已知函数 。
。
(1):当 时,求函数
时,求函数 的极小值;
的极小值;
(2):试讨论函数 零点的个数。
零点的个数。
(本小题13分)
一个多面体的直观图和三视图如图所示,其中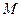 ,
, 分别是
分别是 ,
, 的中点,
的中点, 是
是 上的一动点.
上的一动点.
(Ⅰ)求该几何体的体积与表面积;
(Ⅱ)求证: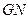 ⊥
⊥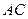 ;
;
(Ⅲ)当 时,在棱
时,在棱 上确定一点
上确定一点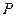 ,使得
,使得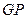 //平面
//平面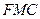 ,并给出证明.
,并给出证明.
(本小题13分)
已知等比数列 满足
满足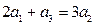 ,且
,且 是
是 ,
, 的等差中项.
的等差中项.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若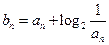 ,
,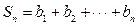 ,求使
,求使  成立的正整数
成立的正整数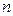 的最小值.
的最小值.
(本小题13分)
已知向量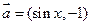 ,
,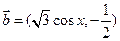 ,函数
,函数 .
.
(Ⅰ)求函数 的最小正周期
的最小正周期 ;
;
(Ⅱ)已知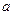 ,
, ,
, 分别为
分别为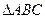 内角
内角 ,
,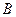 ,
,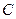 的对边,其中
的对边,其中 为锐角,
为锐角,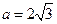 ,
,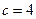 ,且
,且 ,求
,求 ,
, 和
和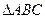 的面积
的面积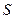 .
.
(本题满分15分) 设抛物线C1:x2=4y的焦点为F,曲线C2与C1关于原点对称.
(Ⅰ) 求曲线C2的方程;
(Ⅱ) 曲线C2上是否存在一点P(异于原点),过点P作C1的两条切线PA,PB,切点A,B,满足| AB |是 | FA | 与 | FB | 的等差中项?若存在,求出点P的坐标;若不存在,请说明理由
(本题满分15分) 已知函数f(x)= x3+ax2+bx,a , b
x3+ax2+bx,a , b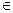 R.
R.
(Ⅰ) 曲线C:y=f(x) 经过点P(1,2),且曲线C在点P处的切线平行于直线y=2x+1,求a,b的值;
(Ⅱ) 已知f(x)在区间(1,2) 内存在两个极值点,求证:0<a+b<2