(本小题满分12分)在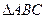 中,角
中,角 、
、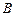 、
、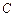 所对应的边分别为
所对应的边分别为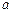 、
、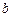 、
、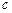 ,且满足
,且满足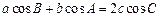 ,
,
(I)求角C的值;
(II)若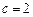 ,求
,求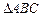 面积的最大值.
面积的最大值.
(本小题满分12分)锐角 中,角
中,角 所对的边分别为
所对的边分别为 ,已知
,已知 ,(Ⅰ)求
,(Ⅰ)求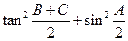 的值;(Ⅱ)若
的值;(Ⅱ)若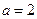 ,
, ,求
,求 的值.
的值.
(本小题满分14分)
现有甲,乙,丙,丁四名篮球运动员进行传球训练,由甲开始传球(即第一次传球是由甲传向乙或丙或丁),记第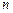 次传球球传回到甲的不同传球方式种数为
次传球球传回到甲的不同传球方式种数为 .
.
(1)试写出 ,
, 并找出
并找出 与
与 (
( )的关系式;
)的关系式;
(2)求数列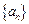 的通项公式;
的通项公式;
(3)证明:当 时,
时, 
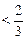 .
.
(本小题满分13分)
(1)若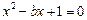 (
( ),试求实数
),试求实数 的范围;
的范围;
(2)设实数 ,函数
,函数 ,
,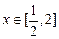
试求函数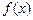 的值域。
的值域。
(本小题满分12分)
已知不等式组 所表示的平面区域为D
所表示的平面区域为D ,记D
,记D 内的整点个数为
内的整点个数为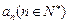 (整点即横坐标和纵坐标均为整数的点).
(整点即横坐标和纵坐标均为整数的点).
(1)数列 的通项
的通项 公式
公式 ;
;
(2)若 ,记
,记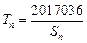 ,求证:
,求证: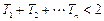 .
.
(本小题满分12分)
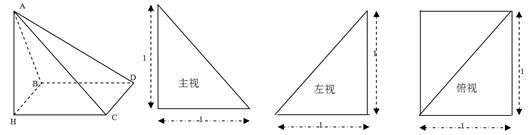
如左图示,在四棱锥A-BHCD中,AH⊥面BHCD,此棱锥的三视图如下:
(1)求二面角B-AC-D的大小;
(2)在线段AC上是否存在一点E,使ED与面BCD成45°角?若存在,确定E的位置;若不存在,说明理由。