已知向量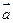 =(1,
=(1,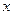 ),
),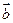 =(
=(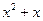 ,
,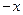 ),m为常数且m≤-2,
),m为常数且m≤-2,
求使不等式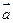 ·
·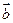 +2>m
+2>m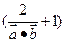 成立的
成立的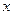 的范围.
的范围.
已知函数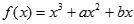 在
在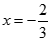 与
与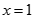 处都取得极值.
处都取得极值.
(1)求函数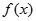 的解析式;
的解析式;
(2)求函数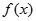 在区间[-2,2]的最大值与最小值.
在区间[-2,2]的最大值与最小值.
如图,边长为2的正方形ACDE所在的平面与平面ABC垂直,AD与CE的交点为M,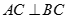 ,且AC=BC.
,且AC=BC.
(1)求证: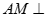 平面EBC;
平面EBC;
(2)求二面角 的大小.
的大小.
已知
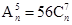 ,且(1-2x)n=a0+a1x+a2x2+a3x3++anxn.
,且(1-2x)n=a0+a1x+a2x2+a3x3++anxn.
(1)求n的值;
(2)求a1+a2+a3++an的值.
已知直线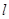 的参数方程为
的参数方程为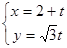 (
( 为参数),曲线
为参数),曲线 的极坐标方程为
的极坐标方程为
(1)求曲线 的普通方程;
的普通方程;
(2)求直线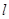 被曲线
被曲线 截得的弦长.
截得的弦长.
在等比数列{an}中,an>0(n∈N*),且a1a3=4,a3+1是a2和a4的等差中项.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足bn=an+1+log2an(n=1,2,3,…),求数列{bn}的前n项和Sn.