如图,矩形BCC1B1所在平面垂直于三角形AB C所在平面,BB1=CC
C所在平面,BB1=CC 1=AC=2,
1=AC=2,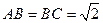 ,又E、F分别是C1A和C1B的中点。
,又E、F分别是C1A和C1B的中点。
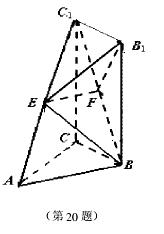 (1)求证:EF//平面ABC;
(1)求证:EF//平面ABC;
(2)求证:平面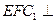 平面C1CBB1;
平面C1CBB1;
(3)求异面直线AB与EB1所成的角。
设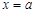 和
和 是函数
是函数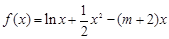 的两个极值点,其中
的两个极值点,其中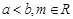 .
.
(1)求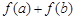 的取值范围;
的取值范围;
(2)若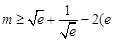 为自然对数的底数),求
为自然对数的底数),求 的最大值.
的最大值.
已知 分别为椭圆
分别为椭圆 的上、下焦点,
的上、下焦点, 是抛物线
是抛物线 的焦点,点
的焦点,点 是
是 与
与 在第二象限的交点, 且
在第二象限的交点, 且
(1)求椭圆 的方程;
的方程;
(2)与圆 相切的直线
相切的直线 交椭
交椭 于
于 ,若椭圆
,若椭圆 上一点
上一点 满足
满足 ,求实数
,求实数 的取值范围.
的取值范围.
如图,矩形 是一个观光区的平面示意图,建立平面直角坐标系,使顶点
是一个观光区的平面示意图,建立平面直角坐标系,使顶点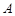 在坐标原点
在坐标原点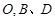 分别为
分别为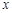 轴、
轴、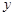 轴,
轴,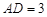 (百米),
(百米),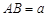 (百米)(
(百米)(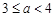 )观光区中间叶形阴影部分
)观光区中间叶形阴影部分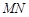 是一个人工湖,它的左下方边缘曲线是函数
是一个人工湖,它的左下方边缘曲线是函数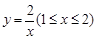 的图象的一段.为了便于游客观光,拟在观光区铺设一条穿越该观光区的直路(宽度不计),要求其与人工湖左下方边缘曲线段
的图象的一段.为了便于游客观光,拟在观光区铺设一条穿越该观光区的直路(宽度不计),要求其与人工湖左下方边缘曲线段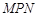 相切(切点记为
相切(切点记为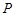 ),并把该观光区分为两部分,且直线
),并把该观光区分为两部分,且直线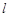 左下部分建设为花圃.记点
左下部分建设为花圃.记点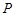 到
到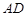 的距离为
的距离为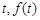 表示花圃的面积.
表示花圃的面积.
(1)求花圃面积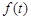 的表达式;
的表达式;
(2)求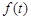 的最小值.
的最小值.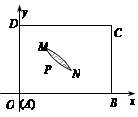
如图,在四棱锥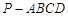 中,
中,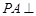 平面
平面 ,
,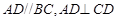 ,且
,且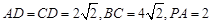 ,点
,点 在
在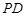 上.
上.
(1)求证: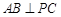 ;
;
(2)若二面角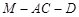 的大小为
的大小为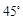 ,求
,求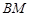 与平面
与平面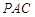 所成角的正弦值.
所成角的正弦值.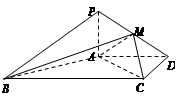
甲、乙两人参加某种选拔测试.在备选的10道题中,甲答对其中每道题的概率都是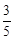 ,乙能答对其中5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,至少得15分才能入选.
,乙能答对其中5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,至少得15分才能入选.
(1)求乙得分的分布列和数学期望;
(2)求甲、乙两人中至少有一人入选的概率.