选修4—2:矩阵与变换
二阶矩阵M有特征值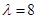 ,其对应的一个特征向量e=
,其对应的一个特征向量e=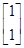 ,并且矩阵M对应的变换将点
,并且矩阵M对应的变换将点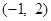
变换成点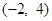 ,求矩阵M.
,求矩阵M.
(本小题满分12分)(1)解关于x的不等式:(x – 1)2>a(x – 2) + 1(a∈R).
(2)命题p: 使不等式
使不等式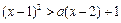 成立;命题q:
成立;命题q: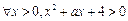 恒成立.已知p或q为真,求实数a的取值范围.
恒成立.已知p或q为真,求实数a的取值范围.
(本小题满分12分)连续抛掷同一颗均匀的骰子,令第i次得到的点数为ai,若存在正整数k,使a1 + a2 +…+ak = 6,则称k为你的幸运数字.(1)求你的幸运数字为4的概率;(2)若k = 1,则你的得分为6分;若k = 2,则你的得分为4分;若k = 3,则你的得分为2分;若抛掷三次还没找到你的幸运数字则记0分.求得分 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)已知△ABC的三个内角分别为A、B、C,向量m = (sinB, 1 – cosB)与向量n= (2,0)夹角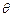 的余弦值为
的余弦值为 .(1)求角B的大小;(2)求sinA + sinC的取值范围.
.(1)求角B的大小;(2)求sinA + sinC的取值范围.
(本小题满分13分)已知函数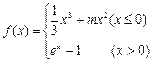 (1)讨论函数f (x)的极值情况;(2)设g (x) = ln(x + 1),当x1>x2>0时,试比较f (x1 – x2)与g (x1 – x2)及g (x1) –g (x2)三者的大小;并说明理由.
(1)讨论函数f (x)的极值情况;(2)设g (x) = ln(x + 1),当x1>x2>0时,试比较f (x1 – x2)与g (x1 – x2)及g (x1) –g (x2)三者的大小;并说明理由.
已知集合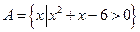 ,
,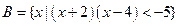 ,
,
又 ;
;
(1)求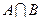 及
及
(2) ,求m的取值范围。
,求m的取值范围。