若给定椭圆C：ax2+by2=1(a>0,b>0,a
b)和点N(x0,y0)，则称直线l：ax0x+by0y=1为椭圆C的“伴随直线”，
(1)若N(x0,y0)在椭圆C上，判断椭圆C与它的“伴随直线”的位置关系(当直线与椭圆的交点个数为0个、1个、2个时，分别称直线与椭圆相离、相切、相交)，并说明理由；
(2)命题：“若点N(x0,y0)在椭圆C的外部，则直线l与椭圆C必相交.”写出这个命题的逆命题，判断此逆命题的真假，说明理由；
(3)若N(x0,y0)在椭圆C的内部，过N点任意作一条直线，交椭圆C于A、B，交l于M点(异于A、B)，设
，
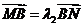，问
是否为定值？说明理由.
是椭圆
上的动点。
的取值范围
恒成立，求实数a的取值范围。
的不等式
的极坐标方程为
，圆C的方程为
是定义在
上的增函数，如果不等式
对于任意
恒成立，求实数
的取值范围；
恒成立，求实数
的取值范围．
前n项和为
，且
满足
且
（n≥1），求数列