(本小题满分12分)
如图,在棱长为1的正方体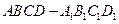 中,
中, 是侧棱
是侧棱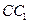 上的一点,
上的一点, .
.
(1) 试确定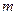 ,使直线
,使直线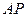 与平面
与平面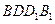
所成角的正切值为 ;
;
(2) 在线段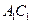 上是否存在一个定点
上是否存在一个定点 ,
,
使得对任意的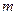 ,
,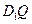 在平面
在平面 上
上
的射影垂直于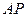 ,并证明你的结论.
,并证明你的结论.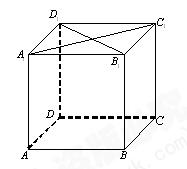
抛物线的顶点在原点,以 轴为对称轴,经过焦点且倾斜角为
轴为对称轴,经过焦点且倾斜角为 的直线,被抛物线所截得的弦长为
的直线,被抛物线所截得的弦长为 ,试求抛物线方程.
,试求抛物线方程.
抛物线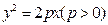 上点
上点 到定点
到定点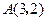 和焦点
和焦点 的距离之和的最小值为
的距离之和的最小值为 ,求此抛物线的方程.
,求此抛物线的方程.
某体育馆拟用运动场的边角地建一个矩形的健身室.如图所示,ABCD是一块边长为50 m的正方形地皮,扇形CEF是运动场的一部分,其半径为40 m,矩形AGHM就是拟建的健身室,其中G、M分别在AB和AD上,H在 上.设矩形AGHM的面积为S,∠HCF=θ,请将S表示为θ的函数,并指出当点H在
上.设矩形AGHM的面积为S,∠HCF=θ,请将S表示为θ的函数,并指出当点H在 的何处时,该健身室的面积最大,最大面积是多少?
的何处时,该健身室的面积最大,最大面积是多少?
已知函数y=sin2x+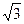 cos2x-2.
cos2x-2.
(1)用“五点法”作出函数在一个周期内的图象;
(2)求这个函数的周期和单调区间;
(3)求函数图象的对称轴方程.
(4)说明图象是由y=sinx的图象经过怎样的变换得到的.
a为何值时,方程sin2x+2sinxcosx-2cos2x=a有实数解.