抛物线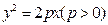 上点
上点 到定点
到定点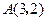 和焦点
和焦点 的距离之和的最小值为
的距离之和的最小值为 ,求此抛物线的方程.
,求此抛物线的方程.
函数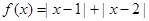
(1)画出函数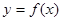 的图象;
的图象;
(2)若不等式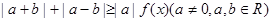 恒成立,求实数
恒成立,求实数 的范围.
的范围.
如图,四边形 是圆内接四边形,延长
是圆内接四边形,延长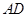 与的延长线
与的延长线 交于点
交于点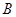 ,且
,且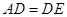 ,
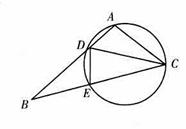
, 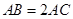 .
.
(1)求证: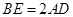 ;
;
(2)当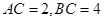 时,求
时,求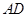 的长.
的长.
已知函数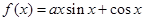 ,且
,且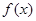 在
在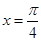 处的切线斜率为
处的切线斜率为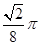 .
.
(1)求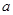 的值,并讨论
的值,并讨论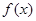 在
在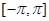 上的单调性;
上的单调性;
(2)设函数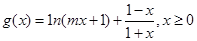 ,其中
,其中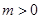 ,若对任意的
,若对任意的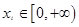 总存在
总存在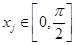 ,使得
,使得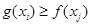 成立,求
成立,求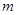 的取值范围.
的取值范围.
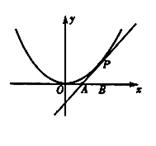
如图,已知直线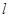 与抛物线
与抛物线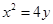 相切于点
相切于点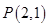 ,且与
,且与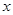 轴交于点
轴交于点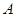 ,
,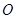 为坐标原点,定点
为坐标原点,定点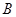 的坐标为
的坐标为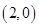 .
. 
(1)若动点 满足
满足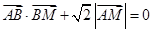 ,求点
,求点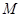 的轨迹
的轨迹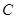 ;
;
(2)若过点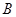 的直线
的直线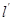 (斜率不等于零)与(1)中的轨迹
(斜率不等于零)与(1)中的轨迹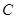 交于不同的两点
交于不同的两点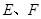 (
(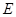 在
在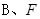 之间),试求△OBE与△OBF面积之比的取值范围.
之间),试求△OBE与△OBF面积之比的取值范围.
如图所示的几何体中,四边形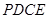 为矩形,
为矩形,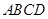 为直角梯形,且
为直角梯形,且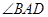 =
= 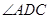 = 90°,平面
= 90°,平面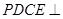 平面
平面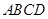 ,
,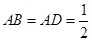 ,
,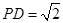
(1)若 为
为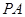 的中点,求证:
的中点,求证: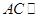 平面
平面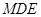 ;
;
(2)求平面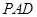 与平面
与平面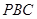 所成锐二面角的大小.
所成锐二面角的大小.