(本小题满分12分)
已知双曲线过点P ,它的
,它的 渐近线方程为
渐近线方程为
(1)求双曲线的标准方程;
(2)设F1和F2是这双曲线的左、右焦点,点P在这双曲线上,且|PF1|·|PF2|=32,求∠F1PF2的大小.
已知点A,B的坐标分别是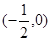 ,
, ,直线AM,BM相交于点M,且直线AM的斜率与直线BM的斜率的差是-1.
,直线AM,BM相交于点M,且直线AM的斜率与直线BM的斜率的差是-1.
(1)过点M的轨迹C的方程;
(2)过原点作两条互相垂直的直线 .
.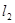 分别交曲线C于点A,C和B,D,求四边形ABCD面积的最小值.
分别交曲线C于点A,C和B,D,求四边形ABCD面积的最小值.
在如图所示的几何体中,AE⊥平面ABC,CD∥AE,F是BE的中点,AC=BC=1,∠ACB=90°,AE=2CD=2.
(1)证明DF⊥平面ABE;
(2)求二面角A-BD-E的余弦值.
在△ABC中,角A,B,C的对边分别为a,b,c,且A,B,C成等差数列.
(1)若b= ,a=3,求c的值;
,a=3,求c的值;
(2)设t=sinAsinC,求t的最大值.
已知定义域为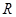 的函数
的函数 是奇函数.
是奇函数.
(Ⅰ)求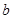 的值;
的值;
(Ⅱ)判断函数 的单调性,并用定义证明;
的单调性,并用定义证明;
(Ⅲ)若对任意的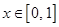 ,不等式
,不等式 恒成立,求实数
恒成立,求实数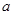 的取值
的取值
范围.
已知函数 (
(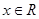 ),其中
),其中 ,
, ,
,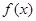 满足以下两个条件:①两条相邻对称轴之间的距离为
满足以下两个条件:①两条相邻对称轴之间的距离为 ;②
;②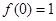 .
.
(Ⅰ)求函数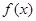 的解析式;
的解析式;
(Ⅱ)求函数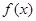 在
在 内的单调递增区间;
内的单调递增区间;
(Ⅲ)若方程 在
在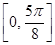 内有
内有 个不等实根,求实数
个不等实根,求实数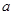 的取值范围.
的取值范围.