在如图所示的几何体中,AE⊥平面ABC,CD∥AE,F是BE的中点,AC=BC=1,∠ACB=90°,AE=2CD=2.
(1)证明DF⊥平面ABE;
(2)求二面角A-BD-E的余弦值.
如图,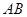 是圆
是圆 的直径,
的直径,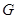 是
是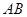 延长线上的一点,
延长线上的一点,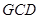 是圆
是圆 的割线,过点
的割线,过点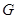 作
作 的垂线,交直线
的垂线,交直线 于点
于点 ,交直线
,交直线 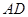 于点
于点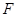 ,过点
,过点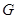 作圆
作圆 的切线,切点为
的切线,切点为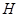 .
.
如图, 是⊙
是⊙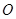 的直径,
的直径, 是⊙
是⊙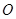 的切线,
的切线, 与
与 的延长线交于点
的延长线交于点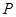 ,
, 为切点.若
为切点.若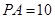 ,
, ,
, 的平分线
的平分线 与
与 和⊙
和⊙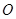 分别交于点
分别交于点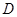 、
、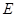 ,求
,求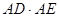 的值.
的值.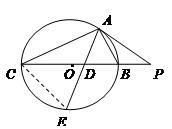
如图,D,E分别为△ABC的边AB,AC上的点,且不与△ABC的顶点重合.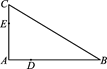
已知AE的长为m,AC的长为n,AD,AB的长是关于x的方程x2-14x+mn=0的两个根.
(1)证明:C,B,D,E四点共圆;
(2)若∠A=90°,且m=4,n=6,求C,B,D,E所在圆的半径.
如图,A,B,C,D四点在同一圆上,AD的延长线与BC的延长线交于E点,EC=ED.
(1)证明:CD∥AB;
(2)延长CD到F,延长DC到G,使得EF=EG,证明:A,B,G,F四点共圆.
如图,D,E分别为△ABC边AB,AC的中点,直线DE交△ABC的外接圆于F,G两点.若CF∥AB,证明:
(1)CD=BC;
(2)△BCD∽△GBD.