椐统计从化机械厂生产一种汽车曲轴,由于受生产能力和技术水平的限制,会产生一些次品,该厂生产这种产品的次品率 与日产量x(单位:件)之满足关系
与日产量x(单位:件)之满足关系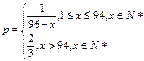 。已知每生产一件合格品可盈利3000元,但每生产一件次品将亏损1500元。
。已知每生产一件合格品可盈利3000元,但每生产一件次品将亏损1500元。
(Ⅰ)判断日产量x超过94时,生产这种产品能否盈利?并说明理由;
(Ⅱ)当日产量x不超过94时,将该厂生产这种产品每天的盈利额y(元)表示成日产量x的函数;为了获得最高日盈利额,日产量应定为多少件?
(本小题满分14分)
设函数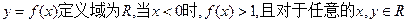 ,有
,有 。
。
(1)求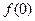 的值;(2)求数列
的值;(2)求数列 的通项公式;(3)是否存在正数
的通项公式;(3)是否存在正数 均成立,若存在,求出k的最大值,并证明,否则说明理由。
均成立,若存在,求出k的最大值,并证明,否则说明理由。
(本小题满分12分)


|
|
如图,A为椭圆 上
上
|
|
 的一个动点,弦AB、AC分别过焦点
的一个动点,弦AB、AC分别过焦点
|
F1、F2。当AC垂直于x轴时,恰好
|
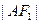 ∶
∶ =3∶1.
=3∶1.
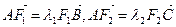 ,试判断
,试判断 是否为定值?若是,则求出该定值;若不是,请说明理由。
是否为定值?若是,则求出该定值;若不是,请说明理由。
(本小题满分12分)在正方体 中,棱长
中,棱长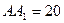 .
.
(1)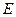 为棱
为棱 的中点,求证:
的中点,求证: ;
;
(2)求二面角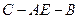 的大小;
的大小;
(3)求点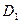 到平面
到平面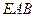 的距离.
的距离.
(本小题满分12分)已知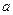 为实数,函数
为实数,函数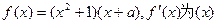 的导函数。(1)若
的导函数。(1)若 上的最大值和最小值;(2)若函数
上的最大值和最小值;(2)若函数 有两个不同的极值点,求
有两个不同的极值点,求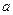 的取值范围。
的取值范围。
(本小题满分12分)
甲、乙两名射击运动员,甲射击一次命中10环的概率为 ,乙射击一次命中10环的概率为s,若他们各自独立地射击两次,设乙命中10环的次数为ξ,且ξ的数学期望Eξ=
,乙射击一次命中10环的概率为s,若他们各自独立地射击两次,设乙命中10环的次数为ξ,且ξ的数学期望Eξ= ,
, 表示甲与乙命中10环的次数的差的绝对值.
表示甲与乙命中10环的次数的差的绝对值.
(1)求s的值及 的分布列, (2)求
的分布列, (2)求 的数学期望.
的数学期望.