（本小题满分12分）已知定点C（-1，0）及椭圆
，过点C的动直线与椭圆相交于A，B两点。
（1）若线段AB中点的横坐标是
，求直线AB的方程；
（2）在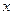
轴上是否存在点M，使
为常数？若存在，求出点M的坐标；若不存在，请说明理由。
已知函数
.
（1）证明：
；
（2）证明：
.
（本小题满分12分）
已知直线
：
和椭圆
，椭圆C的离心率为
，连结椭圆的四个顶点形成四边形的面积为
.
（1）求椭圆C的方程；
（2）若直线与椭圆C有两个不同的交点，求实数m的取值范围；
（3）当
时，设直线与y轴的交点为P，M为椭圆C上的动点，求线段PM长度的最大值.
如图，在四棱柱
中，底面ABCD和侧面
都是矩形，E是CD的中点，
，
.
（1）求证：
；
（2）若
，求三棱锥
的体积.
由某种设备的使用年限
（年）与所支出的维修费
（万元）的数据资料算得如下结果，
，
，
，
.
（1）求所支出的维修费y对使用年限x的线性回归方程
；
（2）①判断变量x与y之间是正相关还是负相关；
②当使用年限为8年时，试估计支出的维修费是多少.
（附：在线性回归方程中，）
，
，其中
，
为样本平均值.)
将函数
的图形向右平移
个单位后得到
的图像，已知的部分图像如图所示，该图像与y轴相交于点
，与x轴相交于点P、Q，点M为最高点，且
的面积为
.
（1）求函数的解析式；
（2）在
中，
分别是角A，B，C的对边，
，且
，求面积的最大值.