由某种设备的使用年限 (年)与所支出的维修费
(年)与所支出的维修费 (万元)的数据资料算得如下结果,
(万元)的数据资料算得如下结果, ,
, ,
, ,
, .
.
(1)求所支出的维修费y对使用年限x的线性回归方程 ;
;
(2)①判断变量x与y之间是正相关还是负相关;
②当使用年限为8年时,试估计支出的维修费是多少.
(附:在线性回归方程 中,)
中,) ,
, ,其中
,其中 ,
, 为样本平均值.)
为样本平均值.)
(本小题满分14分)已知函数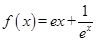
(Ⅰ)求函数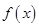 的最小值;
的最小值;
(Ⅱ)若对所有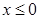 都有
都有 ,求实数
,求实数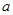 的取值范围.
的取值范围.
【原创】(本小题满分12分)已知椭圆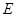 短轴的端点为
短轴的端点为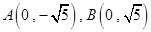 ,且椭圆上的点到焦点的最小距离是
,且椭圆上的点到焦点的最小距离是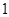 .
.
(Ⅰ)求椭圆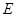 的标准方程;
的标准方程;
(Ⅱ)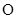 为原点,
为原点,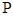 是椭圆
是椭圆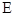 上异于
上异于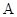 、
、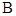 的任意一点,直线
的任意一点,直线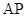 ,
,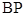 分别交
分别交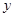 轴于
轴于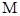 ,
,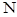 ,问
,问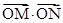 是否为定值,说明理由.
是否为定值,说明理由.
【改编】(本小题满分12分)在数列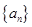 中,已知
中,已知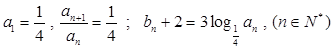
(Ⅰ)求数列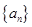 、
、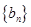 的通项公式;
的通项公式;
(Ⅱ)设数列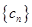 满足
满足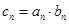 ,求
,求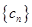 的前n项和
的前n项和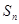 .
.
【改编】(本小题满分12分)已知三棱柱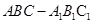 中,侧棱垂直于底面,
中,侧棱垂直于底面,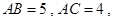
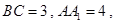 点
点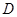 在
在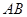 上.
上.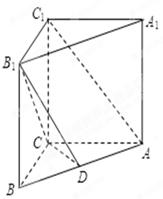
(Ⅰ)若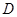 是
是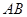 中点,求证:
中点,求证: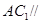 平面
平面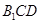 ;
;
(Ⅱ)当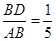 时,求三棱锥
时,求三棱锥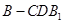 的体积.
的体积.
(本小题满分12分)为了解甲、乙两厂的产品质量,分别从两厂生产的产品中各随机抽取10件,测量产品中某种元素的含量(单位:毫克),其测量数据的茎叶图如下: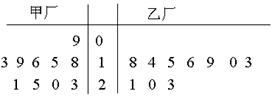
规定:当产品中此种元素含量大于18毫克时,认定该产品为优等品.
(Ⅰ)试比较甲、乙两厂生产的产品中该种元素含量的平均值的大小;
(Ⅱ)现从乙厂抽出的非优等品中随机抽取两件,求至少抽到一件该元素含量为10毫克或13毫克的产品的概率.