(本小题满分15分)已知椭圆 的左焦点为F,左右顶点分别为A、C,
的左焦点为F,左右顶点分别为A、C,
上顶点为B,过F,B,C三点作 ,其中圆心P的坐标为
,其中圆心P的坐标为 .
.
(1) 若椭圆的离心率 ,求
,求 的方程;
的方程;
(2)若 的圆心在直线
的圆心在直线 上,求椭圆的方程.
上,求椭圆的方程.
(本小题14分)二次函数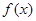 满足
满足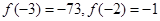 ,且对称轴
,且对称轴
(1)求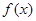 ; (2)求不等式
; (2)求不等式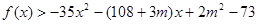
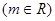 的解集.
的解集.
(本小题12分)设等差数列{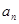 }的前
}的前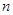 项和为
项和为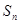 ,已知
,已知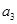 =
=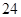 ,
,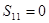 .
.
(1) 求数列{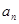 }的通项公式; (2)当n为何值时,
}的通项公式; (2)当n为何值时,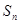 最大,并求
最大,并求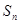 的最大值.
的最大值.
(本小题12分)已知锐角三角形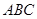 的内角
的内角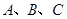 的对边分别为
的对边分别为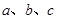 ,
,
且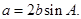
(1)求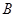 的大小;
的大小;
(2)若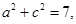 三角形ABC的面积为1 ,求
三角形ABC的面积为1 ,求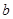 的值.
的值.
(本小题满分14分)如果函数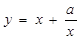 有如下性质:如果常数a>0,那么该函数在
有如下性质:如果常数a>0,那么该函数在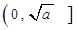 上是减函数,在
上是减函数,在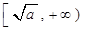 上是增函数
上是增函数
(本小题满分14分)已知f(x)是定义在( 0,+∞)上的增函数,
且f( ) = f(x)-f(y)
) = f(x)-f(y)
(1)求f(1)的值;
(2)若f(6)= 1,解不等式 f( x+3 )-f(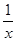 ) <2
) <2