.某工厂去年某产品的年产量为100万只,每只产品的销售价为10元,固定成本为8元.今年,工厂第一次投入100万元(科技成本),并计划以后每年比上一年多投入100万元(科技成本),预计产量年递增10万只,第n次投入后,每只产品的固定成本为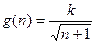 (k>0,k为常数,
(k>0,k为常数,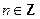 且n≥0),若产品销售价保持不变,第n次投入后的年利润为
且n≥0),若产品销售价保持不变,第n次投入后的年利润为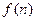 万元.
万元.
(1)求k 的值,并求出
的值,并求出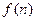 的表达式;
的表达式;
(2)问从今年算起第几年利润最高?最高利润为多少万元?
已知数列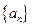 中,
中,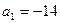 ,
,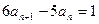 ,
,
(1) 证明:
证明: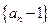 是等比数列;
是等比数列;
(2)若数列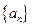 的前
的前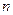 项和为
项和为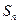 ,求数列
,求数列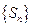 的通项公式,并求出n为何值时,
的通项公式,并求出n为何值时,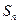 取得最小值,并说明理由。(参考数据:
取得最小值,并说明理由。(参考数据: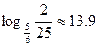 )
)
.
某校从高一年级学生中随机抽取60名学生,将其期中考试的数学成绩(均为整数)分成六段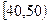 ,
,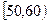 ,…,
,…,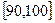 后得到如下频率分布直方图.
后得到如下频率分布直方图.
(1)求分数在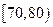 内的频率;
内的频率;
(2)用分层抽样的方法在80分以上(含80分)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任意选取2人,求其中恰有1人的分数不低于90分的概率.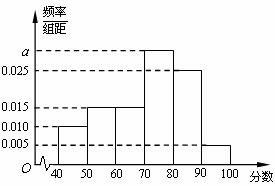
.以下是粤西地区某县搜集到的新房屋的销售价格 和
和 房屋的面积
房屋的面积 的数据:
的数据:
(1)画出数据散点图;
(2)由散点图判断新房屋销售价格y和房屋面积x是否具有线性相关关系?若有,求线性回 归方程。(保留四位小数)
归方程。(保留四位小数)
(3)根据房屋面积预报销售价格的回归方程,预报房屋面积为 时的销售价格。
时的销售价格。
参考公式:  ,
,
参考数据: ,
,
 ,
,
.在△ABC中,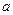 ,b,c分别是三个内角A,B,C所对边,若
,b,c分别是三个内角A,B,C所对边,若 ,
,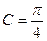 ,
,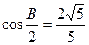 ,求△ABC的面积S.
,求△ABC的面积S.