(本小题满分12分)
在 中,角A、B、C所对的边分别为
中,角A、B、C所对的边分别为 ,且
,且
(1)求C和 ;
;
(2)P为 内任一点(含边界),点P到三边距离之和为
内任一点(含边界),点P到三边距离之和为 ,设P到AB,BC距离分别为
,设P到AB,BC距离分别为 ,用
,用 表示
表示 并求
并求 的
的 取值范围。
取值范围。
(本小题12分)为调查某地区老人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
| 性别是否需要志愿者 |
男 |
女 |
| 需要 |
40 |
30 |
| 不需要 |
160 |
270 |
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)能否有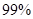 的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
(3)根据(2)的结论,能否提供更好的调查方法来估计该地区老年人,需要志愿帮助的老人的比例?说明理由. 附: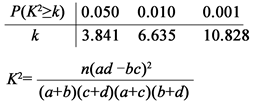
菱形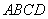 中,
中, ,且
,且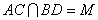 ,现将三角形
,现将三角形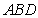 沿着
沿着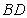 折起形成四面体
折起形成四面体 ,如图所示.
,如图所示.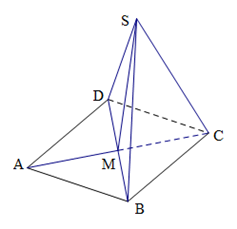
(1)当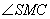 为多大时,
为多大时,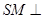 面
面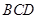 ?并证明;
?并证明;
(2)在(1)的条件下,求点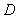 到面
到面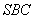 的距离.
的距离.
为了解某校高三学生的视力情况,随机抽查了该校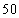 名高三学生,得到如图所示的频率分布直方图.
名高三学生,得到如图所示的频率分布直方图.
(1)求图中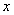 的值;
的值;
(2)若从视力在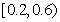 的学生中随机选取
的学生中随机选取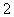 人,求这2人视力均在
人,求这2人视力均在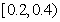 的概率
的概率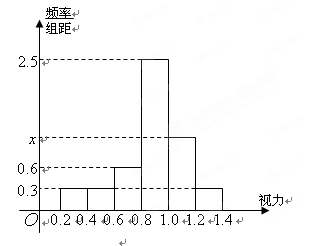
已知曲线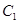 的极坐标方程是
的极坐标方程是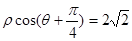 ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为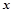 轴的正半轴,建立平面直角坐标系,曲线
轴的正半轴,建立平面直角坐标系,曲线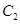 的参数方程是:
的参数方程是: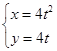 (
(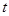 是参数).
是参数).
(1)将曲线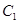 和曲线
和曲线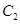 的方程转化为普通方程;
的方程转化为普通方程;
(2)若曲线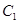 与曲线
与曲线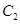 相交于
相交于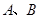 两点,求证
两点,求证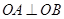 ;
;
(3)设直线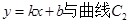 交于两点
交于两点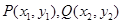 ,且
,且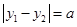 (
(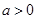 且
且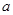 为常数),过弦
为常数),过弦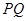 的中点
的中点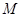 作平行于
作平行于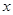 轴的直线交曲线
轴的直线交曲线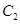 于点
于点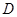 ,求证:
,求证: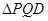 的面积是定值.
的面积是定值.
已知函数 .
.
(1)当 且
且 ,
, 时,试用含
时,试用含 的式子表示
的式子表示 ,并讨论
,并讨论 的单调区间;
的单调区间;
(2)若 有零点,
有零点, ,且对函数定义域内一切满足
,且对函数定义域内一切满足 的实数
的实数 有
有 .
.
①求 的表达式;
的表达式;
②当 时,求函数
时,求函数 的图像与函数
的图像与函数 的图像的交点坐标.
的图像的交点坐标.