设函数
在
,
处取得极值,且
.
(Ⅰ)若
,求
的值,并求
的单调区间;
(Ⅱ)若
,求
的取值范围.
(本小题满分14分)已知函数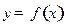 满足:
满足: ;(1)分别写出
;(1)分别写出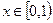 时
时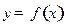 的解析式
的解析式 和
和 时
时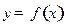 的解析式
的解析式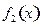 ;并猜想
;并猜想 时
时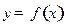 的解析式
的解析式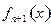 (用
(用 和
和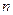 表示)(不必证明)(2)当
表示)(不必证明)(2)当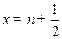
 时,
时,
 的图象上有点列
的图象上有点列 和点列
和点列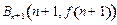 ,线段
,线段 与线段
与线段 的交点
的交点 ,求点
,求点 的坐标
的坐标 ;
;
(3)在前面(1)(2)的基础上,请你提出一个点列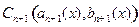 的问题,并进行研究,并写下你研究的过程
的问题,并进行研究,并写下你研究的过程
(本小题满分12分)
有一幅椭圆型彗星轨道图,长4cm,高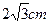 ,如下图,
,如下图,
已知O为椭圆中心,A1,A2是长轴两端点,
|
太阳位于椭圆的左焦点F处.
(Ⅰ)建立适当的坐标系,写出椭圆方程,(本小题满分12分)某地一水库年初有水量a(a≥10000),其中含污染物的量为p0(设水与污染物混合均匀),已知该地降水量与月份的关系为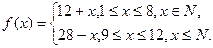 而每月流入水库的污水量与蒸发的水量都是r,且此污水中含污染物的量为p(p<r),设当年水库中的水不作它用.
而每月流入水库的污水量与蒸发的水量都是r,且此污水中含污染物的量为p(p<r),设当年水库中的水不作它用.
(Ⅰ)求第x月水库中水的含污比g(x)的表达式(含污比= );
);
(Ⅱ)当p0=0时,求水质量差的月份及此月的含污比.
(本小题满分12分)已知数列{an}的前n项和为Sn, 且满足条件:4S n =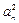 + 4n – 1 , nÎN*.
+ 4n – 1 , nÎN*.
(1) 证明:(a n– 2)2 –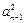 ="0" (n ³ 2);(2) 满足条件的数列不惟一,试至少求出数列{an}的的3个不同的通项公式 .
="0" (n ³ 2);(2) 满足条件的数列不惟一,试至少求出数列{an}的的3个不同的通项公式 .
(本小题满分12分)
已知函数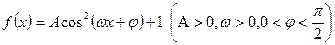 的最大值为3,
的最大值为3,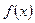 的图像的相邻两对称轴间的距离为2,在Y轴上的截距为2.
的图像的相邻两对称轴间的距离为2,在Y轴上的截距为2.
(Ⅰ)求函数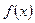 的解析式;(Ⅱ)设数列
的解析式;(Ⅱ)设数列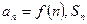 为其前n项和,求
为其前n项和,求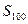 .
.