已知椭圆 的离心率为
的离心率为 ,右焦点
,右焦点 也是抛物线
也是抛物线 的焦点。
的焦点。
(1)求椭圆方程;
(2)若直线 与
与 相交于
相交于 、
、 两点。
两点。
①若 ,求直线
,求直线 的方程;
的方程;
②若动点 满足
满足 ,问动点
,问动点 的轨迹能否与椭圆
的轨迹能否与椭圆 存在公共点?若存在,求出点
存在公共点?若存在,求出点 的坐标;若不存在,说明理由。
的坐标;若不存在,说明理由。
如图,圆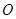 的两弦
的两弦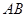 和
和 交于点
交于点 ,
,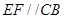 ,
,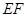 交
交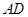 的延长线于点
的延长线于点 .求证:△
.求证:△ ∽△
∽△ .
.
各项均为正数的数列{an}中,设 ,
, ,且
,且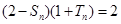 ,
,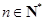 .
.
(1)设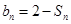 ,证明数列{bn}是等比数列;
,证明数列{bn}是等比数列;
(2)设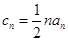 ,求集合
,求集合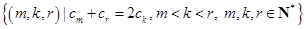 .
.
已知函数 在
在 时取得极小值.
时取得极小值.
(1)求实数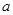 的值;
的值;
(2)是否存在区间 ,使得
,使得 在该区间上的值域为
在该区间上的值域为 ?若存在,求出
?若存在,求出 ,
, 的值;
的值;
若不存在,说明理由.
如图,在平面直角坐标系xOy中,椭圆 的离心率为
的离心率为 ,过椭圆右焦点
,过椭圆右焦点 作两条互相垂直的弦
作两条互相垂直的弦 与
与 .当直线
.当直线 斜率为0时,
斜率为0时, .
.
(1)求椭圆的方程;
(2)求 的取值范围.
的取值范围.
某风景区在一个直径AB为100米的半圆形花园中设计一条观光线路(如图所示).在点A与圆
弧上的一点C之间设计为直线段小路,在路的两侧边缘种植绿化带;从点C到点B设计为沿弧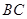 的弧形小路,在路的一侧边缘种植绿化带.(注:小路及绿化带的宽度忽略不计)
的弧形小路,在路的一侧边缘种植绿化带.(注:小路及绿化带的宽度忽略不计)
(1)设 (弧度),将绿化带总长度表示为
(弧度),将绿化带总长度表示为 的函数
的函数 ;
;
(2)试确定 的值,使得绿化带总长度最大.
的值,使得绿化带总长度最大.