设计如图所示一水渠,它的横截面曲线是抛物线形, 宽2m,渠
宽2m,渠 深为1.5m,水面EF距AB为0.5m. (1)求截面图中水面宽度;
深为1.5m,水面EF距AB为0.5m. (1)求截面图中水面宽度; (2)由于情况有变,现要将此水渠改造为横截面是等腰梯形,要求渠深不变,不准往回填土,只准挖土,试求截面梯形的下边长为多大时,才能使所挖的土最少?
(2)由于情况有变,现要将此水渠改造为横截面是等腰梯形,要求渠深不变,不准往回填土,只准挖土,试求截面梯形的下边长为多大时,才能使所挖的土最少?
(本小题10分)已知圆心 的坐标为(1,1),圆
的坐标为(1,1),圆 与
与 轴和
轴和 轴都相切.
轴都相切.
(1)求圆 的方程;
的方程;
(2)求与圆 相切,且在
相切,且在 轴和
轴和 轴上的截距相等的直线方程.
轴上的截距相等的直线方程.
已知圆 ,圆
,圆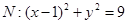 ,动圆
,动圆 与圆
与圆 外切并且与圆
外切并且与圆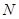 内切,圆心
内切,圆心 的轨迹为曲线
的轨迹为曲线 .
.
(1)求曲线 的轨迹方程;
的轨迹方程;
(2) 是与圆
是与圆 以及圆
以及圆 都相切的一条直线,
都相切的一条直线, 与曲线
与曲线 交于两点
交于两点 ,当圆
,当圆 的半径最长时,
的半径最长时,
求 的长.
的长.
(本小题12分)已知椭圆 的右焦点为
的右焦点为 ,点
,点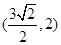 在椭圆上.
在椭圆上.
(Ⅰ)求椭圆的离心率;
(Ⅱ)点 在圆
在圆 上,且
上,且 在第一象限,过
在第一象限,过 作圆
作圆 的切线交椭圆于
的切线交椭圆于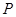 ,
, 两点,求证:△
两点,求证:△ 的周长是定值.
的周长是定值.
(本小题12分)已知圆 直线
直线
(Ⅰ)求证:直线 与圆C相交;
与圆C相交;
(Ⅱ)计算直线 被圆
被圆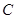 截得的最短的弦长.
截得的最短的弦长.
(本小题12分)如图,在直三棱柱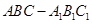 中,
中, ,
, 是棱
是棱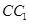 上的动点,
上的动点,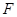 是
是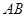 中点,
中点, ,
, .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)若二面角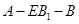 的大小是
的大小是 ,求
,求 的长.
的长.