(本小题满分16分)已知函数 .
.
(Ⅰ)当 时,求证:函数
时,求证:函数 在
在 上单调递增;
上单调递增;
(Ⅱ)若函数 有三个零点,求
有三个零点,求 的值;
的值;
(Ⅲ)若存在 ,使得
,使得 ,试求
,试求 的取值范围.
的取值范围.
(本小题满分10分)已知 、
、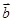 、
、 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中 ,
,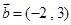 ,
,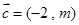
(1)若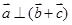 ,求
,求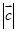 ;
;
(2)若 与
与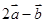 共线,求
共线,求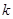 的值.
的值.
(本小题12分)圆C的半径为3,圆心在直线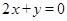 上且在x轴下方,x轴被圆C截得的弦长为
上且在x轴下方,x轴被圆C截得的弦长为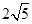 .
.
(1)求圆C的方程;
(2)是否存在斜率为1的直线l,使得以l被圆截得的弦为直径的圆过原点?若存在,求出直线l的方程;若不存在,说明理由.
(本小题12分)已知数列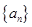 的前n项和为
的前n项和为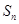 ,
,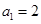 ,
, .
.
(1)求数列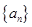 的通项公式;
的通项公式;
(2)求数列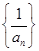 的前n项和
的前n项和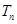 .
.
(本小题12分)某镇计划建造一个室内面积为800m2的矩形蔬菜温室,在温室内,沿左、右两侧与后侧内墙各保留1m宽的通道,沿前侧内墙保留3m宽的空地。当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积是多少?
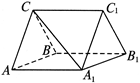
(本小题12分)如图所示,三棱柱ABC-A1B1C1中,
.
(1)证明: ;
;
(2)若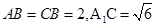 ,求三棱柱ABC-A1B1C1的体积.
,求三棱柱ABC-A1B1C1的体积.