在△ABC中，角A、B、C的对边分别为a，b，c，已知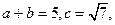
且
（I）求角C的大小；
（II）求△ABC的面积。
正方形ABCD边长为4，点E是边CD上的一点，
将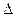
AED沿AE折起到
的位
置时，有平面
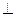平面ABCE，
并且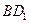
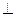
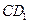（如图）
（I）判断并证明E点的具体位置；（II）
求点D/到平面ABCE的距离．
四棱锥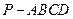
中，底面ABCD是一个平行四边形，
，
，
（1）求四棱锥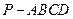的体积；
（2）定义
＝
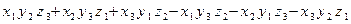，对于向量
，
，
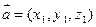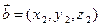有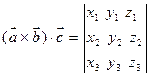
，
则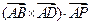
＝__________．
如图，在四棱锥P-ABCD中，平面PAD⊥平面ABCD,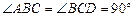 
，
，E是BD的中点．
（1）求证：EC//平面
APD；
（2）求BP与平面A
BCD所成角的正切值；
（3） 求二面角P-AB-D的大小．
如图所示，已知三棱柱ABC-
的底面边长均为2，侧棱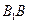
的长为2且与底面ABC所成角为
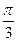，且侧面
垂直于底面ABC．
（1）求二面角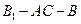
的正切值的大小；
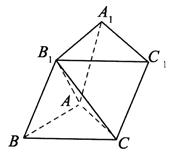（2）若其余条件不变，只改变侧棱的长度，当侧棱
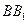的长度为多长时，可使面
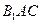和底面垂直．
已知向量
=（
，1），
=（x，x2），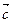
=（－3，－x2+x），函数f（x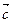）=·（+）．（1）求函数f（x）的解析式与定义域；（2）求函数f（x）的值域．