一汽车厂生产A、B、C三类轿车，每类轿车有豪华型和标准型两种型号，某月生产情况如下表（单位：辆）
| |
轿车A |
轿车B |
轿车C |
| 舒适型 |
100 |
150 |
x |
| 标准型 |
300 |
450 |
600 |
按分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
（I）求x的值；
（I）列出所有基本事件，并求出至少有一辆是豪华型轿车的概率.
已知直线
经过直线
与直线
的交点
，且垂直于直线
．
（1）求直线的方程；
（2）求直线关于原点
对称的直线方程．
已知函数
（其中
且
），
是
的反函数．
（1）已知关于
的方程
在
上有实数解，求实数
的取值范围；
（2）当
时，讨论函数
的奇偶性和单调性；
（3）当，
时，关于的方程
有三个不同的实数解，求的取值范围．
某工厂某种航空产品的年固定成本为
万元，每生产
件，需另投入成本为
，当年产量不足
件时，
（万元）．当年产量不小于件时，
（万元）．每件商品售价为
万元．通过市场分析，该厂生产的商品能全部售完．
（1）写出年利润
（万元）关于年产量（件）的函数解析式；
（2）年产量为多少件时，该厂在这一商品的生产中所获利润最大？
已知幂函数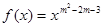
（
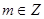）在
是单调减函数，且为偶函数．
（1）求
的解析式；
（2）讨论
的奇偶性，并说明理由．
设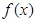
是定义在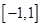
上函数，且对任意
，当
时，都有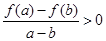
成立．解不等式
．