如图，三棱锥S—ABC中，AB⊥BC，D、E分别为AC、BC的中点，SA=SB=SC。
（1）求证：BC⊥平面SDE；
（2）若AB=BC=2，SB=4，求三棱锥S—ABC的体积。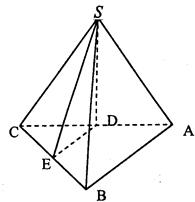
直线l的方程为（a＋1）x＋y＋2－a＝0（a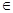
R）。
（1）若l在两坐标轴上的截距相等，求a的值；
（2）若l不经过第二象限，求实数a的取值范围。
如图，四棱锥P—ABCD的底面是正方形，PD⊥底面ABCD，点E在棱PB上。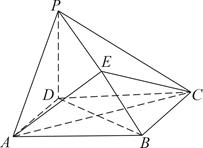
（1）求证：平面AEC⊥PDB；
（2）当PD＝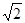
AB且E为PB的中点时，求AE与平面PDB所成角的大小。
已知△ABC中，A（1，1），B（m，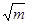
），C（4，2），1＜m＜4。
求m为何值时，△ABC的面积S最大。
在锐角△ABC中，a、b、c分别为角A、B、C所对的边，又c＝
，b＝4，且BC边上的高h＝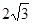
。
（1）求角C；
（2）求边a。
选修4—5：不等式选讲
已知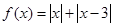
，若不等式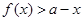
恒成立，求实数
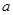的取值范围.