（本小题满分12分）
为援助汶川灾后重建，对某项工程进行竞标，共有6家企业参与竞标，其中A企业来自辽宁省，B、C两家企业来自福建省，D、E、F三家企业来自河南省，此项工程需要两家企业联合施工，假设每家企业中标的概率相同。
（1）企业E中标的概率是多少？
（2）在中标的企业中，至少有一家来自河南省的概率是多少
某人投篮一次命中概率为
，共投篮7次。
（1）试问至多有1次命中的概率；
（2）试问出现命中次数为奇数的概率与命中次数为偶数的概率是否相等？请说明理由。
已知函数
（
，
），且函数
的最小正周期为
．
(Ⅰ)求函数的解析式并求的最小值；
(Ⅱ)在
中，角A，B，C所对的边分别为
，若
=1，
,且
，求边长
．
已知函数f(x)=kx+b的图象与x、y轴分别相交于点A、B,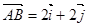
(
、
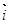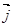分别是与x、y轴正半轴同方向的单位向量), 函数g(x)=x2-x-6.
(1)求k、b的值;
(2)当x满足f(x)> g(x)时,求函数
的最小值.
已知方程
的方程
，直线
（1）求
的取值范围； （2）若圆与直线交于P、Q两点，且以PQ为直径的圆恰过坐标原点，求实数m的值．
汽车制造厂生产A、B、C三类轿车，每类轿车均有舒适型和标准型两种型号，某月的产量如下表（单位：辆）
| 轿车A |
轿车B |
轿车C |
|
| 舒适型 |
100 |
150 |
Z |
| 标准型 |
300 |
450 |
600 |
按类用分层抽样的方法在这个月生产的轿车中抽取50辆，其中有A类轿车10辆。
（1）求Z的值；
（2）用分层抽样的方法在C类轿车中抽取一个容量为5的样本，将该样本看成一个总体，从中任取2辆，求至少有一辆舒适型轿车的概率；
（3）用随机抽样的方法从B类舒适型轿车中抽取8辆，经检测它们的得分如下：9.4，8.6，9.2，9.6，8.7,9.3,9.0,8.2。把这8辆轿车的得分看成一个总体，从中任取一个数，求该数与样本平均数之差的绝对值不超过0.5的概率。