(本小题满分12分)某校高一年级有四个班,其中一、二班为数学课改班,三、四班为数学非课改班.在期末考试中,课改班与非课改班的数学成绩优秀与非优秀人数统计如下表.
| 优秀 |
非优秀 |
总计 |
|
| 课改班 |
50 |
||
| 非课改班 |
20 |
110 |
|
| 合计 |
210 |
(1)请完成上面的2´2列联表,并判断若按99%的可靠性要求,能否认为“成绩与课改
有关”;
(2)把全部210人进行编号,从编号中有放回抽取4次,每次抽取1个,记被抽取的4
人中的优秀人数为x,若每次抽取的结果是相互独立的,求x的分布列及数学期望Ex.
(本小题满分12分)已知函数 .
.
(1)求函数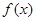 的最小正周期;
的最小正周期;
(2)若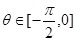 ,
,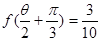 ,求
,求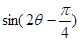 的值.
的值.
(本小题12分)第(1)小题5分,第(2)题7分
已知中心在原点 ,左焦点为
,左焦点为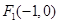 的椭圆C的左顶点为
的椭圆C的左顶点为 ,上顶点为
,上顶点为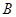 ,
,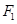 到直线
到直线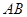 的距离为
的距离为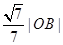 .
.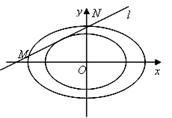
(1)求椭圆C的方程;
(2)若椭圆 方程为:
方程为: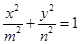 (
(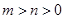 ),椭圆
),椭圆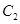 方程为:
方程为: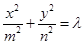 (
(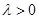 ,且
,且 ),则称椭圆
),则称椭圆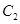 是椭圆
是椭圆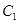 的
的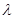 倍相似椭圆.已知
倍相似椭圆.已知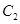 是椭圆C的
是椭圆C的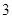 倍相似椭圆,若椭圆C的任意一条切线
倍相似椭圆,若椭圆C的任意一条切线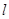 交椭圆
交椭圆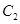 于两点
于两点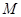 、
、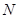 ,试求弦长
,试求弦长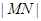 的取值范围.
的取值范围.
(本小题12分)第(1)小题5分,第(2)题7分
在平面直角坐标系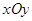 中,点
中,点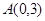 ,直线
,直线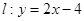 ,设圆
,设圆 的半径为
的半径为 ,圆心在
,圆心在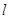 上.
上.
(1)若圆心 也在直线
也在直线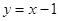 上,过点
上,过点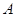 作圆
作圆 的切线,求切线的方程;
的切线,求切线的方程;
(2)若圆 上存在点
上存在点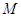 ,使
,使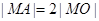 ,求圆心
,求圆心 的横坐标
的横坐标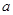 的取值范围.
的取值范围.
(本小题12分)第(1)小题5分,第(2)题7分
如图,在四棱锥中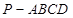 中,底面
中,底面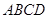 为菱形,
为菱形,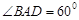 ,
, ,点
,点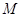 在线段
在线段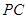 上,且
上,且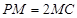 ,
,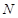 为
为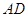 的中点.
的中点.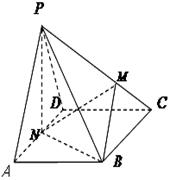
(1)求证: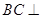 平面
平面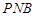 ;
;
(2)若平面 平面
平面 ,求三棱锥
,求三棱锥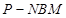 的体积;
的体积;