(本小题12分)第(1)小题5分,第(2)题7分
已知中心在原点 ,左焦点为
,左焦点为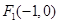 的椭圆C的左顶点为
的椭圆C的左顶点为 ,上顶点为
,上顶点为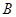 ,
,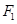 到直线
到直线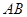 的距离为
的距离为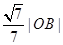 .
.
(1)求椭圆C的方程;
(2)若椭圆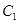 方程为:
方程为: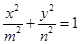 (
(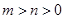 ),椭圆
),椭圆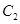 方程为:
方程为: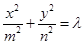 (
(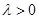 ,且
,且 ),则称椭圆
),则称椭圆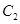 是椭圆
是椭圆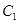 的
的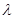 倍相似椭圆.已知
倍相似椭圆.已知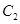 是椭圆C的
是椭圆C的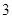 倍相似椭圆,若椭圆C的任意一条切线
倍相似椭圆,若椭圆C的任意一条切线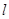 交椭圆
交椭圆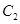 于两点
于两点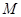 、
、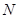 ,试求弦长
,试求弦长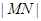 的取值范围.
的取值范围.
已知数列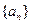 和
和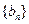 满足
满足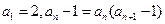 ,
,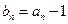 ,数列
,数列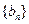 的前
的前 和为
和为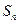 .
.
(1)求数列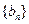 的通项公式;
的通项公式; (2)设
(2)设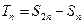 ,求证:
,求证: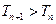 ;
;
(3)求证:对任意的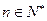 有
有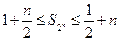 成立.
成立.
设函数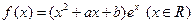 .
.
(1)若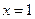 是函数
是函数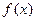 的一个极值点,试求出
的一个极值点,试求出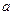 关于
关于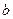 的关系式(用
的关系式(用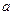 表示
表示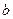 ),并确定
),并确定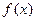 的单调区间;
的单调区间;
(2)在(1)的条件下,设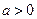 ,函数
,函数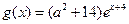 .若存在
.若存在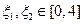 使得
使得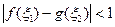 成立,求
成立,求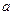 的取值范围.
的取值范围.
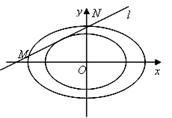
已知点C(1,0),点A、B是⊙O: 上任意两个不同的点,
上任意两个不同的点,
且满足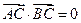 ,设P为弦AB的中点.
,设P为弦AB的中点.
(1)求点P的轨迹T的方程;
(2)试探究在轨迹T上是否存在这样的点:它到直线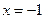 的
的
距离恰好等于到点C的距离?若存在,求出这样的点的坐标;若不存在,
说明理由.
如图,△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行
四边形,DC 平面ABC ,
平面ABC , ,已知AE与平面ABC所成的角为
,已知AE与平面ABC所成的角为 ,
, 且
且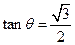 .
.
(1)证明:平面ACD 平面
平面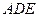 ;
;
(2)记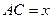 ,
, 表示三棱锥A-CBE的体积,求
表示三棱锥A-CBE的体积,求 的表达式;
的表达式;
(3)当 取得最大值时,求二面角D-AB-C的大小.
取得最大值时,求二面角D-AB-C的大小.
某射击运动员为争取获得2010年广州亚运会的参赛资格正在加紧训练.已知在某次训练中他射击了 枪,每一枪的射击结果相互独立,每枪成绩不低于10环的概率为
枪,每一枪的射击结果相互独立,每枪成绩不低于10环的概率为 ,设
,设 为本次训练中成绩不低于10环的射击次数,
为本次训练中成绩不低于10环的射击次数, 的数学期望
的数学期望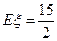 ,方差
,方差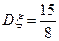 .
.
(1)求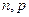 的值;
的值;
(2)训练中教练要求:若有5枪或5枪以上成绩低于10环,则需要补射,求该运动员在本次训练中需要补射的概率.
(结果用分数表示.已知: ,
,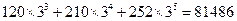 )
)