已知数列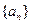 和
和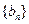 满足
满足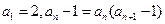 ,
,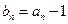 ,数列
,数列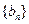 的前
的前 和为
和为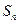 .
.
(1)求数列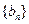 的通项公式;
的通项公式; (2)设
(2)设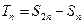 ,求证:
,求证: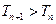 ;
;
(3)求证:对任意的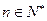 有
有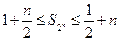 成立.
成立.
设函数 ,其中向量
,其中向量 ,
,
(1)求 的最小正周期与单调减区间;
的最小正周期与单调减区间;
(2)在△ABC中, 分别是角A、B、C的对边,已知
分别是角A、B、C的对边,已知 ,△ABC的面积为
,△ABC的面积为 ,求
,求 的值。
的值。
已知一动圆与圆 外切,同时与圆
外切,同时与圆 内切.
内切.
(1)求动圆圆心 的轨迹方程,并说明它是什么样的曲线;
的轨迹方程,并说明它是什么样的曲线;
(2)直线 与M的轨迹相交于不同的两点
与M的轨迹相交于不同的两点 、
、 ,求
,求 的中点的坐标;
的中点的坐标;
(3)求(2)中△OPQ的面积(O为坐标原点).
已知双曲线的中心在坐标原点,焦点在x轴上,渐近线方程为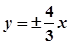 ,且经过点
,且经过点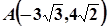 ,设
,设 是双曲线的两个焦点,点
是双曲线的两个焦点,点 在双曲线上,且
在双曲线上,且 =64.
=64.
(1)求双曲线的方程;
(2)求 .
.
已知抛物线以坐标轴为对称轴,原点为顶点,开口向上,且过圆 的圆心.
的圆心.
(1)求此抛物线的方程;
(2)在(1)中所求抛物线上找一点,使这点到直线 的距离最短,并求距离的最小值.
的距离最短,并求距离的最小值.
已知椭圆的标准方程为 .
.
(1)求椭圆的长轴和短轴的大小;
(2)求椭圆的离心率;
(3)求以此椭圆的长轴端点为短轴端点,并且经过点P(-4,1)的椭圆方程.