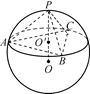
如图,△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行
四边形,DC 平面ABC ,
平面ABC , ,已知AE与平面ABC所成的角为
,已知AE与平面ABC所成的角为 ,
, 且
且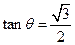 .
.
(1)证明:平面ACD 平面
平面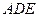 ;
;
(2)记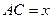 ,
, 表示三棱锥A-CBE的体积,求
表示三棱锥A-CBE的体积,求 的表达式;
的表达式;
(3)当 取得最大值时,求二面角D-AB-C的大小.
取得最大值时,求二面角D-AB-C的大小.
四面体的六条棱中,有五条棱长都等于a.
(1)求该四面体的体积的最大值;
(2)当四面体的体积最大时,求其表面积.
在边长为a的正三角形铁皮的三个角切去三个全等的四边形,再把它的边沿虚线折起(如图),做成一个无盖的正三角形底铁皮箱,当箱底边长为多少时,箱子容积最大?最大容积是多少?
在△ABC中,∠BAC=90°,∠B=60°,AB=1,D为线段BC的中点,E、F为线段AC的三等分点(如图①).将△ABD沿着AD折起到△AB′D的位置,连结B′C(如图②).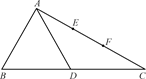
图①
图②
(1)若平面AB′D⊥平面ADC,求三棱锥B′-ADC的体积;
(2)记线段B′C的中点为H,平面B′ED与平面HFD的交线为l,求证:HF∥l;
(3)求证:AD⊥B′E.
如图①所示,在Rt△ABC中,AC=6,BC=3,∠ABC=90°,CD为∠ACB的平分线,点E在线段AC上,CE=4.如图②所示,将△BCD沿CD折起,使得平面BCD⊥平面ACD,连结AB,设点F是AB的中点.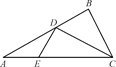 图①
图① 图②
图②
(1)求证:DE⊥平面BCD;
(2)若EF∥平面BDG,其中G为直线AC与平面BDG的交点,求三棱锥B-DEG的体积.
如图,在球面上有四个点P、A、B、C,如果PA、PB、PC两两互相垂直,且PA=PB=PC=a,求这个球的表面积.