如题25图所示,固定的倾角为 = 450、间距为L的光滑金属直杆ce和c'e'与半径为r的竖直光滑绝缘圆弧轨道abc和a'b'c'分别相切于c和c'点,两切点与对应圆心连线与竖直方向夹角也为
= 450、间距为L的光滑金属直杆ce和c'e'与半径为r的竖直光滑绝缘圆弧轨道abc和a'b'c'分别相切于c和c'点,两切点与对应圆心连线与竖直方向夹角也为 = 450,a点和a' 点分别是两圆弧竖直最高点,e点和e'点间用导线连接阻值为R的电阻,在两直杆间cc'和dd'平面区域内有与其垂直的磁场(图中未画出),磁感应强度分布B = B0 sin(
= 450,a点和a' 点分别是两圆弧竖直最高点,e点和e'点间用导线连接阻值为R的电阻,在两直杆间cc'和dd'平面区域内有与其垂直的磁场(图中未画出),磁感应强度分布B = B0 sin(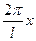 ),式中x为沿直杆向下离开边界dd'的距离,且
),式中x为沿直杆向下离开边界dd'的距离,且 .现
.现
有一长度为L、电阻为R的导体棒在外力F(图中来画出)作用下,以速度v0从磁场边界dd'沿直杆向下匀速通过磁场,到达边界cc'时撤去外力F,导体棒能沿圆弧轨道恰好通过最高处aa' 金属杆电阻、空气阻力不计,重力加速度为g.试求:
(1)导体棒恰好通过圆弧轨道最高处aa' 时的速度大小v;
(2)导体棒匀速运动时的速度v0;
(3)导体棒通过磁场过程中,导体棒上增加的内能.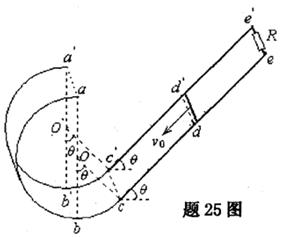
如图所示,一电荷量q=3×10-4C带正电的小球,用绝缘细线悬于竖直放置足够大的平行金属板中的O点.S合上后,小球静止时,细线与竖直方向的夹角α=37°.已知两板相距d=0.1m,电源电动势E=12V,内阻r=2Ω,电阻R1=4Ω,R2=R3= R4 =12Ω,(g=10m/s2,sin370=0.6,cos370=0.8).求:
(1)流过电源的电流强度
(2)两板间的电场强度的大小
(3)小球的质量
如图所示,ABCD为竖立放在场强为E=104 V/m的水平匀强电场中的绝缘光滑轨道,其中轨道的BCD部分是半径为R的半圆环,轨道的水平部分与半圆环相切,A为水平轨道上的一点,而且AB=R=0.2 m.把一质量m=0.1 kg、带电量q=10-4 C的小球放在水平轨道的A点,由静止开始释放后,在轨道的内侧运动.(取g=10 m/s2)求:
(1)它到达C点时的速度是多大?
(2)若让小球安全通过D点,开始释放点离B点至少多远?
光滑水平面与一半径为R=2.5 m的竖直光滑圆轨道平滑连接,如图所示,物体可以由圆轨道底端阀门(图中未画出)进入圆轨道,水平轨道上有一轻质弹簧,其左端固定在墙壁上,右端与质量为m=0.5 kg的小球A接触但不相连,今向左推小球A压缩弹簧至某一位置后,由静止释放小球A,测得小球A到达圆轨道最高点时对轨道的压力大小为FN=10 N,g=10 m/s2.
(1)求弹簧的弹性势能Ep;
(2)若弹簧的弹性势能Ep=25 J,小球进入圆轨道后阀门关闭,通过计算说明小球会不会脱离圆轨道.若脱离,求在轨道上何处脱离(可用三角函数表示),若不能脱离,求小球对轨道的最大与最小压力的差ΔF.
如图所示,一质量为m=2 kg的滑块从半径为R=0.2 m的光滑四分之一圆弧轨道的顶端A处由静止滑下,A点和圆弧对应的圆心O点等高,圆弧的底端B与水平传送带平滑相接.已知传送带匀速运行的速度为v0=4 m/s,B点到传送带右端C点的距离为L=2 m.当滑块滑到传送带的右端C时,其速度恰好与传送带的速度相同.(g=10 m/s2),求: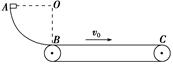
(1)滑块到达底端B时对轨道的压力;
(2)滑块与传送带间的动摩擦因数μ;
(3)此过程中,由于滑块与传送带之间的摩擦而产生的热量Q.
如图所示,质量为m的长木块A静止于光滑水平面上,在其水平的上表面左端放一质量为m的滑块B,已知木块长为L,它与滑块之间的动摩擦因数为μ.现用水平向右的恒力F拉滑块B.
(1)当长木块A的位移为多少时,B从A的右端滑出?
(2)求上述过程中滑块与木块之间产生的内能.