(本小题12分)定义:若函数f(x)对于其定义域内的某一数x0,有f(x0)= x0, 则称x0是f(x)的一个不动点.已知函数f(x)=ax2+(b+1)x+b-1(a≠0).
则称x0是f(x)的一个不动点.已知函数f(x)=ax2+(b+1)x+b-1(a≠0).
(1)当a=1,b=-2时,求函数f(x)的不动点;
(2)若对任意的实数b,函数f(x)恒有两个不动点,求a的取值范围;
(3)在(2)的条件下,若y=f(x)图象上两个点A、B的横坐标是函数f(x)的不动点,且A、B两点关于直线y=kx+ 对称,求b的最小值.
对称,求b的最小值.
(本小题满分12分)某批发市场对某商品的周销售量(单位:吨)进行统计,最近100周的统计结果如下表所示:
| 周销售量 |
2 |
3 |
4 |
| 频数 |
20 |
50 |
30 |
(1)根据上面统计结果,求周销售量分别为2吨,3吨和4吨的频率;
(2)已知每吨该商品的销售利润为2千元,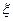 表示该种商品两周销售利润的和(单位:千元),若以上
表示该种商品两周销售利润的和(单位:千元),若以上 述频率作为概率,且各周的销售量相互独立,求
述频率作为概率,且各周的销售量相互独立,求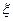 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)已知等差数列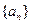 为递增数列,且
为递增数列,且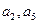 是方程
是方程 的两根,数列
的两根,数列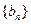 的前
的前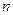 项和
项和 ;
;
(1)求数列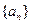 和
和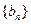 的通项公式;
的通项公式;
(2)若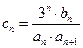 ,
,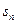 为数列
为数列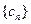 的前n项和,证明:
的前n项和,证明: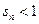
(本小题满分12分)某批发市场对某商品的周销售量(单位:吨)进行统计,最近100周的统计结果如下表所示:
| 周销售量 |
2 |
3 |
4 |
| 频数 |
20 |
50 |
30 |
(1)根据上面统计结果,求周销售量分别为2吨,3吨和4吨的频率;
(2)已知每吨该商品的销售利润为2千元,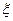 表示该种商品两周销售利润的和(单位:千元),若以上
表示该种商品两周销售利润的和(单位:千元),若以上 述频率作为概率,且各周的销售量相互独立,求
述频率作为概率,且各周的销售量相互独立,求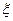 的分布列和数学期望.
的分布列和数学期望.
选修4-5:不等式证明选讲已知函数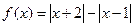 .
.
(Ⅰ)试求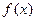 的值域;(Ⅱ)设
的值域;(Ⅱ)设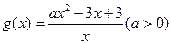 ,若对
,若对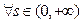 ,
, 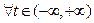 ,恒
,恒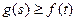 成立,试
成立,试 求实数
求实数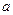 的取值范围
的取值范围
选修4-1:几何证明选讲如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连结FB、FC.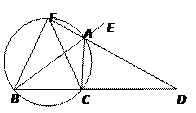
(Ⅰ)求证:FB=FC;
(Ⅱ)求证:FB2=FA·FD;