(本小题满分12分)
已知函数 .
.
(1)确定 在(0,
在(0, +∞)上的单调性;
+∞)上的单调性;
(2)设 在(0,2)上有极值,求a的取值范围.
在(0,2)上有极值,求a的取值范围.
(本小题满分14分)如图,多面体ABCDEF中,平面ADEF⊥平面ABCD,正方形ADEF的边长为2,直角梯形ABCD中,AB∥CD,AD⊥DC,AB=2,CD=4. 
(Ⅰ)求证:BC⊥平面BDE;
(Ⅱ)试在平面CDE上确定点P,使点P到直线DC、DE的距离相等,且AP与平面BEF所成的角等于30°.
(本小题满分13分)国家环境标准制定的空气质量指数(简称AQI)与空气质量等级对应关系如下表:
| 空气质量等级 |
优 |
良 |
轻度污染 |
中度污染 |
重度污染 |
严重污染 |
| AQI值范围 |
[0,50) |
[50,100) |
[100,150) |
[150,200) |
[200,300) |
300及以上 |
下表是由天气网获得的全国东西部各6个城市2015年3月某时刻实时监测到的数据:
| 西部城市 |
AQI数值 |
东部城市 |
AQI数值 |
| 西安 |
108 |
北京 |
104 |
| 西宁 |
92 |
金门 |
42 |
| 克拉玛依 |
37 |
上海 |
x |
| 鄂尔多斯 |
56 |
苏州 |
114 |
| 巴彦淖尔 |
61 |
天津 |
105 |
| 库尔勒 |
456 |
石家庄 |
93 |
| AQI平均值:135 |
AQI平均值:90 |
(Ⅰ)求x的值,并根据上表中的统计数据,判断东、西部城市AQI数值的方差的大小关系(只需写出结果);
(Ⅱ)环保部门从空气质量“优”和“轻度污染”的两类城市随机选取 个城市组织专家进行调研,记选到空气质量“轻度污染”的城市个数为
个城市组织专家进行调研,记选到空气质量“轻度污染”的城市个数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
(本小题满分13分)在平面直角坐标系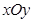 中,设锐角
中,设锐角 的始边与
的始边与 轴的非负半轴重合,终边与单位圆交于点
轴的非负半轴重合,终边与单位圆交于点 ,将射线
,将射线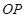 绕坐标原点
绕坐标原点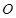 按逆时针方向旋转
按逆时针方向旋转 后与单位圆交于点
后与单位圆交于点 . 记
. 记 .
.
(Ⅰ)求函数 的值域;
的值域;
(Ⅱ)设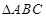 的角
的角 所对的边分别为
所对的边分别为 ,若
,若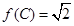 ,且
,且 ,
, ,求
,求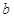 .
.
(本小题满分14分) 已知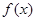 是定义在
是定义在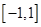 上的奇函数,
上的奇函数,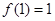 ,且若
,且若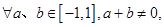 恒有
恒有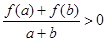 ,
,
(1)证明:函数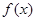 在
在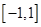 上是增函数;
上是增函数;
(2)解不等式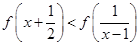 ;
;
(3)若对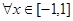 及
及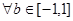 ,不等式
,不等式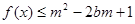 恒成立,求实数
恒成立,求实数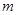 的取值范围.
的取值范围.
(本小题满分14分) 已知向量 ,
,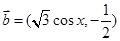 ,函数
,函数 ,
,
(1)求函数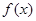 的最小正周期
的最小正周期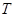 与值域;
与值域;
(2)已知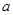 ,
, ,
, 分别为
分别为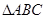 内角
内角 ,
,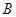 ,
, 的对边,其中
的对边,其中 为锐角,
为锐角, 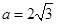 ,
,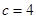 ,且
,且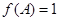 ,求
,求 ,
, 和
和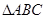 的面积
的面积 .
.