已知数列{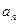 }中,
}中,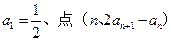 在直线y=x上,其中n=1,2,3….
在直线y=x上,其中n=1,2,3….
(Ⅰ)令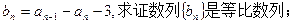
(Ⅱ)求数列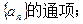
(Ⅲ)设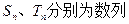
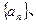
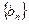 的前n项和,是否存在实数
的前n项和,是否存在实数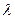 ,使得数列
,使得数列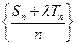 为等差数列?若存在,试求出
为等差数列?若存在,试求出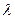 .若不存在,则说明理由。
.若不存在,则说明理由。
在四棱锥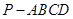 中,底面
中,底面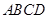 为菱形,其中
为菱形,其中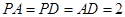 ,
,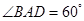 ,
, 为
为 的中点.
的中点.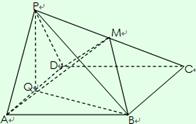
(1)求证: ;
;
(2)若平面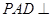 平面
平面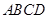 ,且
,且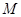 为
为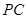 的中点,求四棱锥
的中点,求四棱锥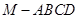 的体积.
的体积.
已知函数 ,曲线
,曲线 上点
上点 处的切线方程为
处的切线方程为 .
.
(1)若 在
在 时有极值,求
时有极值,求 的表达式;
的表达式;
(2)在(1)的条件下求 在
在 上的最值及相应的
上的最值及相应的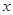 的值.
的值.
已知函数 .
.
(1)求函数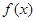 的最小正周期;
的最小正周期;
(2)当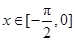 时,求函数
时,求函数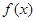 的最大值和最小值.
的最大值和最小值.
对于任意的实数
恒成立,记实数M的最大值是m.
(Ⅰ)求m的值; (Ⅱ)解不等式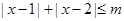 .
.
在直角坐标系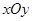 中,曲线
中,曲线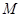 的参数方程为
的参数方程为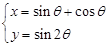 (
(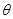
为参数),若以该直角坐标系的原点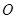 为极点,
为极点,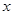 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线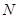 的极坐标方程为:
的极坐标方程为: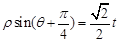 (其中
(其中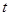 为常数).
为常数).
(Ⅰ)若曲线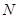 与曲线
与曲线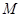 只有一个公共点,求
只有一个公共点,求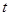 的取值范围;
的取值范围;
(Ⅱ)当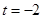 时,求曲线
时,求曲线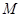 上的点与曲线
上的点与曲线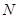 上点的最小距离.
上点的最小距离.