已知函数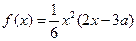 (
( ),
),
(1)当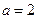 时,求曲线
时,求曲线 在点
在点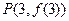 处的切线方程;
处的切线方程;
(2)求函数 在区间
在区间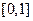 上的最小值.
上的最小值.
有一批数量很大的环形灯管,其次品率为20%,对这批产品进行抽查,每次抽出一件,如果抽出次品,则抽查中止,否则继续抽查,直到抽出次品,但抽查次数最多不超过5次.求抽查次数ξ的分布列.
甲、乙两支足球队鏖战90分钟踢成平局,加时赛30分钟后仍成平局,现决定各派5名队员,每人射一点球决定胜负,设甲、乙两队每个队员的点球命中率均为0.5.
(1)不考虑乙队,求甲队仅有3名队员点球命中,且其中恰有2名队员连续命中的概率;
(2)求甲、乙两队各射完5个点球后,再次出现平局的概率.
为保护水资源,宣传节约用水,某校4名志愿者准备去附近的甲、乙、丙三家公园进行宣传活动,每名志愿者都可以从三家公园中随机选择一家,且每人的选择相互独立.
(1)求4人恰好选择了同一家公园的概率;
(2)设选择甲公园的志愿者的人数为X,试求X的分布列.
某射击小组有甲、乙两名射手,甲的命中率为P1= ,乙的命中率为P2,在射击比赛活动中每人射击两发子弹则完成一次检测,在一次检测中,若两人命中数相等且都不少于一发,则称该射击小组为“先进和谐组”.
,乙的命中率为P2,在射击比赛活动中每人射击两发子弹则完成一次检测,在一次检测中,若两人命中数相等且都不少于一发,则称该射击小组为“先进和谐组”.
(1)若P2= ,求该小组在一次检测中荣获“先进和谐组”的概率;
,求该小组在一次检测中荣获“先进和谐组”的概率;
(2)计划在2013年每月进行1次检测,设这12次检测中该小组获得“先进和谐组”的次数为ξ,如果E(ξ)≥5,求P2的取值范围.
在一场娱乐晚会上,有5位民间歌手(1至5号)登台演唱,由现场数百名观众投票选出最受欢迎歌手.各位观众须彼此独立地在选票上选3名歌手,其中观众甲是1号歌手的歌迷,他必选1号,不选2号,另在3至5号中随机选2名.观众乙和丙对5位歌手的演唱没有偏爱,因此在1至5号中随机选3名歌手.
(1)求观众甲选中3号歌手且观众乙未选中3号歌手的概率;
(2)X表示3号歌手得到观众甲、乙、丙的票数之和,求X的分布列.