某射击小组有甲、乙两名射手,甲的命中率为P1= ,乙的命中率为P2,在射击比赛活动中每人射击两发子弹则完成一次检测,在一次检测中,若两人命中数相等且都不少于一发,则称该射击小组为“先进和谐组”.
,乙的命中率为P2,在射击比赛活动中每人射击两发子弹则完成一次检测,在一次检测中,若两人命中数相等且都不少于一发,则称该射击小组为“先进和谐组”.
(1)若P2= ,求该小组在一次检测中荣获“先进和谐组”的概率;
,求该小组在一次检测中荣获“先进和谐组”的概率;
(2)计划在2013年每月进行1次检测,设这12次检测中该小组获得“先进和谐组”的次数为ξ,如果E(ξ)≥5,求P2的取值范围.
(本小题满分12分)
设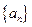 为等比数列,且其满足:
为等比数列,且其满足: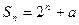 .
.
(1)求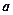 的值及数列
的值及数列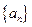 的通项公式;
的通项公式;
(2)已知数列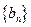 满足
满足 ,求数列
,求数列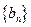 的前n项和
的前n项和 .
.
(本小题满分12分)
已知数列 ,且
,且 是函数
是函数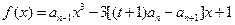 ,(
,( )的一个极值点.数列
)的一个极值点.数列 中
中 (
(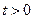 且
且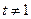 ).
).
(1)求数列 的通项公式;
的通项公式;
(2)记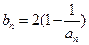 ,当
,当 时,数列
时,数列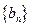 的前
的前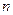 项
项 和为
和为 ,求使
,求使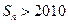 的
的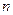 的最小值;
的最小值;
(3)若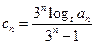 ,证明:
,证明: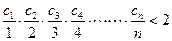 (
(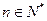 )。
)。
(本小题满分12分)
已知函数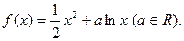
(1)若 上
上 是增函数,求
是增函数,求 的取值范围;
的取值范围;
(2)若 ;
;
(3)若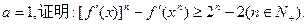
(本小题满分12分)
已知 数列
数列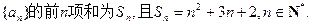
(I)求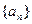 的通项公式;
的通项公式;
(II)由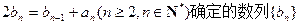 能否为等差数列?若能,求
能否为等差数列?若能,求 的值;若不能,说明理由。
的值;若不能,说明理由。
(本小题满分1 2分)
2分)
四川汶川抗震指挥部决定建造一批简易房(房型为长方体状,房高2.5米),前后墙用2.5米高的彩色钢板,两侧用2.5米高的复合钢板 ,两种钢板的价格都用长度来计算(即:钢板的高均为2.5米,用钢板的长度乘以单价就是这块钢板的价格),每米单价:彩色钢板为450元,复合钢板为200元
,两种钢板的价格都用长度来计算(即:钢板的高均为2.5米,用钢板的长度乘以单价就是这块钢板的价格),每米单价:彩色钢板为450元,复合钢板为200元 .房顶用其它材料建造,每平
.房顶用其它材料建造,每平 方米材料费为200元.每套房材料费控制在32000元以内.
方米材料费为200元.每套房材料费控制在32000元以内.
(1) 设房前面墙的长为
设房前面墙的长为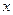 ,两侧墙的长为
,两侧墙的长为 ,所用材料费为
,所用材料费为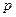 ,试用
,试用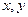 表示
表示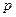 ;
;
(2)简易房面积 的最大值是多少?并求当
的最大值是多少?并求当 最大时
最大时 ,前面墙的长度应设计为多少米?
,前面墙的长度应设计为多少米?