（本小题满分13分）
随机抽取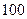
名学生，测得他们的身高（单位：
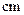），按照区间
，
，
，
，
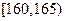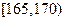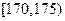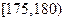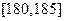分组，得到样本身高的频率分布直方图（如图）．
（Ⅰ）求频率分布直方图中
的值及身高在
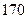
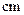以上的学生人数；
（Ⅱ）将身高在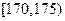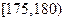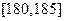，，区间内的学生依次记为
，
，
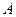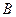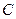三个组，用分层抽样的方法从三个组中抽取
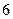人，求从这三个组分别抽取的学生人数；
（Ⅲ）在（Ⅱ）的条件下，要从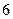名学生中抽取
人，用列举法计算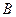组中至少有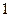
人被抽中的概率．
已知椭圆
的两个焦点分别为
，且
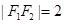，点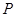
在椭圆上，且
的周长为6.
（1）求椭圆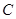
的方程；（2）若点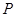的坐标为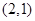
，不过原点
的直线
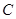与椭圆相交于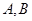
不同两点，设线段
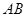的中点为
，且
三点共线．设点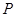到直线的距离为
，求的取值范围．
如图所示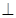，平面
平面
，且四边形为矩形，四边形为直角梯形，
，
，
，
．
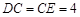（1）求证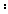
平面
；（2）求平面
与平面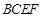
所成锐二面角的余弦值.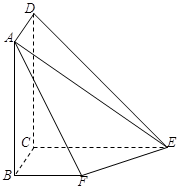
已知数列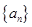
的首项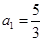
，
，
，
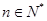（1）求证：数列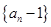
为等比数列；
（2）若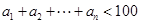
，求最大的正整数
.
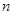在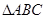
中，角
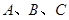所对的边为
，且满足
，
（1）求角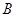
的值；（2）若
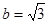且
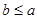，求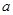
的取值范围.
已知
，其中
．
（1）当
时，证明
；
（2）若
在区间
，
内各有一个根，求
的取值范围；
（3）设数列
的首项
，前
项和
，
，求
，并判断是否为等差数列？