已知双曲线的中心在原点,焦点 在坐标轴上,离心率为
在坐标轴上,离心率为 ,且过点(4,-
,且过点(4,-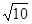 )(1)求双曲线的方程.(2)若点M(3,m)在双曲线上,求证:
)(1)求双曲线的方程.(2)若点M(3,m)在双曲线上,求证: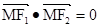 .(3)若点A,B在双曲线上,点N(3,1)恰好是AB的中点,求直线AB的方程(12分)
.(3)若点A,B在双曲线上,点N(3,1)恰好是AB的中点,求直线AB的方程(12分)
已知平行六面体ABCD—A1B1C1D1中,以顶点 A为端点的三条棱长都等于1,两两夹角都是60°,求对角线AC1的长度. (10分)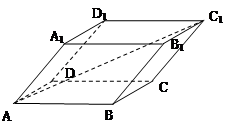
设A、B、C是三角形的三内角,且lgsinA=0,又sinB、sinC是关于x的方程
4x2-2( +1)x+k=0的两个根,求实数k的值.
+1)x+k=0的两个根,求实数k的值.
若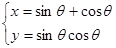 ,试求y=f(x)的解析式.
,试求y=f(x)的解析式.
若f(x)=Asin(x-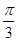 )+B,且f(
)+B,且f(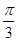 )+f(
)+f(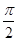 )=7,f(π)-f(0)=2
)=7,f(π)-f(0)=2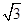 ,求f(x).
,求f(x).