已知函数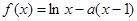 ,
, ∈R.
∈R.
(I)讨论函数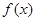 的单调性;
的单调性;
(2)当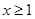 时,
时,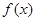 ≤
≤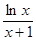 恒成立,求
恒成立,求 的取值范围.
的取值范围.
已知圆C: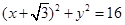 ,点
,点 ,Q是圆上一动点,AQ的垂直平分线交CQ于点M,设点M的轨迹为E。
,Q是圆上一动点,AQ的垂直平分线交CQ于点M,设点M的轨迹为E。
(1)求E的方程;
(2)设P为直线x = 4上不同于点(4,0)的任意一点,D,F分别为曲线E与x轴的左,右两交点,若直线DP与曲线E相交于异于D的点N,证明ΔNPF为钝角三角形.
如图,在直三棱柱ABC—A1B1C1中,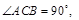
 .
.
(1)若D为AA1中点,求证:平面B1CD 平面B1C1D;
平面B1C1D;
(2)若二面角B1—DC—C1的大小为60°,求AD的长.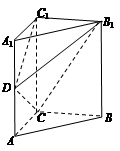
某批发市场对某种商品的日销售量(单位:吨)进行统计,最近50天的统计结果如下表:
| 日销售量(吨) |
1 |
1.5 |
2 |
| 天数 |
10 |
25 |
15 |
若用样本估计总计,以上表频率为概率,且每天的销售量相互独立:
(1)求5天中该种商品恰好有2天的日销售量为1.5吨的概率;
(2)已知每吨该商品的销售利润为2千元,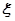 表示该种商品两天销售利润的和(单位:千元),求
表示该种商品两天销售利润的和(单位:千元),求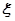 的分布列和数学期望.
的分布列和数学期望.
在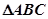 中,内角A, B, C的对边分别为
中,内角A, B, C的对边分别为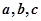 ,已知
,已知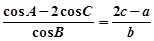 。
。
(1)求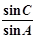 的值;
的值;
(2)若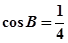 ,
,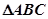 的周长为5, 求b的长度.
的周长为5, 求b的长度.