已知⊙ 的直径为10,
的直径为10, 是⊙
是⊙ 的一条直径,长为20的线段
的一条直径,长为20的线段 的中点
的中点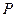 在⊙
在⊙ 上运动(异于
上运动(异于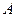 、
、 两点).
两点).
(Ⅰ)求证: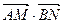 与点
与点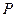 在⊙
在⊙ 上的位置无关;
上的位置无关;
(Ⅱ)当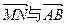 的夹角
的夹角 取何值时,
取何值时,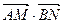 有最大值.
有最大值.
已知矩形 中,
中, ,
, ,
, ,
, 分别在
分别在 ,
, 上,且
上,且 ,
, ,沿
,沿 将四边形
将四边形 折成四边形
折成四边形 ,使点
,使点 在平面
在平面 上的射影
上的射影 在直线
在直线 上.
上.
(1)求证: 平面
平面 ;
;
(2)求二面角 的大小.
的大小.
如图,边长为2的正方形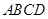 绕
绕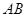 边所在直线旋转一定的角度(小于
边所在直线旋转一定的角度(小于 )到
)到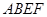 的位置.
的位置.
(1)若 ,求三棱锥
,求三棱锥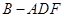 的外接球的表面积;
的外接球的表面积;
(2)若 为线段
为线段 上异于
上异于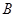 ,
,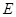 的点,
的点,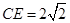 ,设直线
,设直线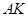 与平面
与平面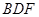 所成角为
所成角为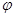 ,当
,当 时,求
时,求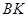 的取值范围.
的取值范围.
如图,四棱锥 中,底面
中,底面 是平行四边形,
是平行四边形, 平面
平面 ,垂足为
,垂足为 ,
, 在线段
在线段 上,
上, ,
, ,
, ,
, 是
是 的中点,四面体
的中点,四面体 的体积为
的体积为 .
.
(1)求异面直线 与
与 所成角的余弦值;
所成角的余弦值;
(2)棱 上是否存在一点
上是否存在一点 ,使
,使 ,若存在,求
,若存在,求 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
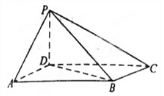
如图,四棱锥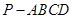 中,底面
中,底面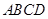 为平行四边形,
为平行四边形, ,
, ,
,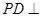 底面
底面 .
.
(1)证明:平面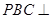 平面
平面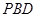 ;
;
(2)若二面角 为
为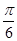 ,求
,求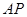 与平面
与平面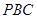 所成的正弦值.
所成的正弦值.
如图,在七面体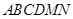 中,四边形
中,四边形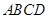 是边长为2的正方形,
是边长为2的正方形,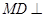 平面
平面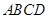 ,
,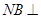 平面
平面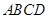 ,且
,且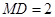 ,
, ,
,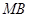 与
与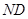 交于
交于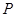 点,点
点,点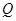 在
在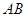 上,且
上,且

(1)求证: 平面
平面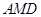 ;
;
(2)求七面体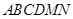 的体积.
的体积.