(本题14分)设函数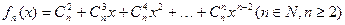 ,当
,当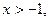 且
且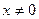 时,证明:
时,证明: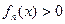 恒成立
恒成立
如图,在极坐标系中, ,求直线
,求直线 的极坐标方程。
的极坐标方程。
已知二次函数 同时满足:⑴不等式
同时满足:⑴不等式 的解集有且只有一个元素;⑵在定义域内存在
的解集有且只有一个元素;⑵在定义域内存在 ,使得不等式
,使得不等式 成立。设数列
成立。设数列 的前
的前
(1)求数列 的通项公式;
的通项公式;
(2)设
(3)设各项均不为零的数列 中,所有满足
中,所有满足 的正整数i的个数称为这个数列
的正整数i的个数称为这个数列 的变号数.另
的变号数.另
.已知向量 ,ω>0,记函数
,ω>0,记函数 =
= ,若
,若 的最小正周期为
的最小正周期为 .
.
⑴ 求ω的值;
⑵ 设△ABC的三边a、b、c满足b2=ac,且边b所对的角为 ,求
,求 的范围,
的范围,
并求此时函数 的值域。
的值域。
已知函数 .
.
(1)若 在
在 [1,+∞
[1,+∞ 上是增函数,求实数
上是增函数,求实数 的取值范围;
的取值范围;
(2)若x=3是 的极值点,求
的极值点,求 在
在 [1,
[1, ]上的最小值和最大值.
]上的最小值和最大值.
过点T(2,0)的直线 交抛物线y2=4x于A、B两点.
交抛物线y2=4x于A、B两点.
(I)若直线l交y轴于点M,且 当m变化时,求
当m变化时,求 的值;
的值;
(II)设A、B在直线 上的射影为D、E,连结AE、BD相交于一点N,则当m变化时,点N为定点的充要条件是n=-2.
上的射影为D、E,连结AE、BD相交于一点N,则当m变化时,点N为定点的充要条件是n=-2.