某陶瓷厂准备烧制甲、乙、丙三件不同的工艺品，制作过程必须先后经过两次烧制，当第一次烧制合格后方可进入第二次烧作，两次烧制过程相互独立，根据该厂现有的技术水平，经过第一次烧制后，甲、乙、丙三件产品合格的概率依次为0.5,0.6,0.4经
过第二
次烧制后，甲、乙、丙三件产品合格的概率依次为0.6,0.5,0.75。
（1）求第一次烧制后恰有一件产品合格的概率；
（2）经过前后两次烧制后，合格工艺品的个数为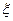
，求随机变量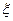的期望。
21． (本小题满分12分)
已知函数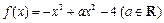
．
(1)若函数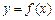
的图象在点P（1，
）处的切线的倾斜角为
，求实数a的值；
(2)设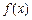
的导函数是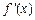
，在 (1) 的条件下，若
，求
的最小值．
(3)若存在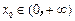
，使
，求a的取值范围．
20． (本小题满分12分)
已知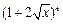
的展开式中，某一项的系数是它前一项系数的2倍，而等于它后一项的系数的
．
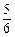(1)求该展开式中二项式系数最大的项；
(2)求展开式中系数最大的项．
19． (本小题满分12分)
如图，直四棱柱ABCD—A1B1C1D1的高为3，底面是边长为4且∠DAB = 60°的菱形，AC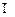
BD = O，A1C1
B1D1 = O1，E是O1A的中点．
(1)求二面角O1－BC－D的大小；
(2)求点E到平面O1BC的距离．
|
18． (本小题满分13分)
已知函数
．
(1)若
在x = 0处取得极值为 – 2，求a、b的值；
(2)若在
上是增函数，求实数a的取值范围．
17． (本小题满分13分)
某工厂在试验阶段大量生产一种零件．这种零件有
、
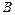两项技术指标需要检测，设各项技术指标达标与否互不影响．若有且仅有一项技术指标达标的概率为
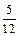，至少一项技术指标达标的概率为
．按质量检验规定：两项技术指标都达标的零件为合格品．
(1)求一个零件经过检测为合格品的概率是多少？
(2)任意依次抽出5个零件进行检测，求其中至多3个零件是合格品的概率是多少？
