19. (本小题满分12分)
如图,直四棱柱ABCD—A1B1C1D1的高为3,底面是边长为4且∠DAB = 60°的菱形,AC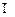 BD = O,A1C1
BD = O,A1C1 B1D1 = O1,E是O1A的中点.
B1D1 = O1,E是O1A的中点.
(1) 求二面角O1-BC-D的大小;
(2) 求点E到平面O1BC的距离.
|
已知函数 是定义在
是定义在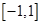 上的奇函数,若对于任意
上的奇函数,若对于任意 ,都有
,都有 且
且 >0时,有
>0时,有 >0
>0
(1)证明: 在
在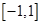 上为单调递增函数;
上为单调递增函数;
(2)解不等式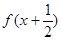 <
< ;
;
已知 是方程
是方程 的两个不等实根,函数
的两个不等实根,函数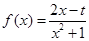 的定义域为
的定义域为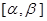 .
.
(1)证明: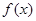 在其定义域上是增函数;
在其定义域上是增函数;
(2)求函数 ;
;
(3)对于(2),若已知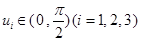 且
且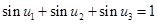 ,证明:
,证明: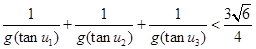 .
.
已知定义在 上的奇函数
上的奇函数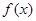 满足
满足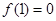 ,且在
,且在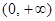 上是增函数. 又函数
上是增函数. 又函数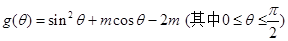
(1)证明: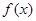 在
在 上也是增函数;
上也是增函数;
(2)若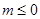 ,分别求出函数
,分别求出函数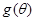 的最大值和最小值;
的最大值和最小值;
(3)若记集合 ,
, ,求
,求 .
.
关于函数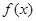 的性质叙述如下:①
的性质叙述如下:①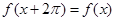 ;②
;②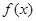 没有最大值;③
没有最大值;③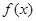 在区间
在区间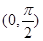 上单调递增;④
上单调递增;④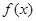 的图象关于原点对称.问:
的图象关于原点对称.问:
(1)函数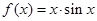 符合上述那几条性质?请对照以上四条性质逐一说明理由.
符合上述那几条性质?请对照以上四条性质逐一说明理由.
(2)是否存在同时符合上述四个性质的函数?若存在,请写出一个这样的函数;若不存在,请说明理由.
已知函数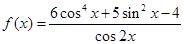
(1)求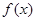 的定义域并判断它的奇偶性;
的定义域并判断它的奇偶性;
(2)求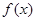 的值域.
的值域.