已知:以点C (t, )(t∈R , t≠ 0) 为圆心的圆与
为圆心的圆与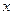 轴交于点O, A,与y轴交于点O, B,其中O为原点.
轴交于点O, A,与y轴交于点O, B,其中O为原点.
(1)求证:△OAB的面积为定值;
(2)设直线y = –2x+4与圆C交于点M, N,若OM = ON,求圆C的方程.
如图,已知菱形 ,其边长为2,
,其边长为2, ,
, 绕着
绕着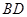 顺时针旋转
顺时针旋转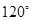 得到
得到 ,
, 是
是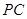 的中点.
的中点.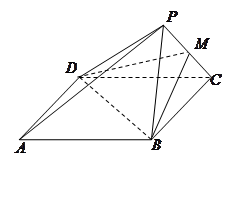
(1)求证: 平面
平面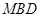 ;
;
(2)求直线 与平面
与平面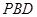 所成角的正弦值.
所成角的正弦值.
已知数列 为等差数列,
为等差数列, ,数列
,数列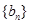 满足
满足 ,且
,且 .(1)求通项公式
.(1)求通项公式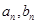 ;(2)设数列
;(2)设数列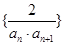 的前
的前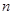 项和为
项和为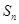 ,试比较
,试比较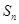 与
与 的大小.
的大小.
已知函数 .
.
(1)求函数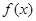 的对称轴方程和单调递增区间;
的对称轴方程和单调递增区间;
(2)若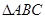 中,
中,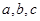 分别是角
分别是角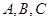 的对边,且
的对边,且 ,
,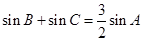 ,求
,求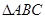 的面积.
的面积.
若存在实常数 和
和 ,使得函数
,使得函数 和
和 对其定义域上的任意实数
对其定义域上的任意实数 分别满足:
分别满足: 和
和 ,则称直线
,则称直线 为
为 和
和 的“隔离直线”.已知
的“隔离直线”.已知 ,
, 为自然对数的底数).
为自然对数的底数).
(Ⅰ)求 的极值;
的极值;
(Ⅱ)函数 和
和 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
已知数列 的前
的前 项和为
项和为 ,且对任意的
,且对任意的 都有
都有 ,
,
(Ⅰ)求数列 的前三项
的前三项 ;
;
(Ⅱ)猜想数列 的通项公式
的通项公式 ,并用数学归纳法证明
,并用数学归纳法证明