一次高中数学期末考试,选择题共有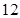 个,每个选择题给出了四个选项,在给出的四个选项中,只有一项是符合题目要求的. 评分标准规定:对于每个选择题,不选或多选或错选得
个,每个选择题给出了四个选项,在给出的四个选项中,只有一项是符合题目要求的. 评分标准规定:对于每个选择题,不选或多选或错选得 分,选对得
分,选对得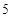 分.在这次考试的选择题部分,某考生比较熟悉其中的
分.在这次考试的选择题部分,某考生比较熟悉其中的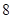 个题,该考生做对了这
个题,该考生做对了这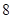 个题.其余
个题.其余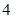 个题,有一个题,因全然不理解题意,该考生在给出的四个选项中,随机选了一个;有一个题给出的四个选项,可判断有一个选项不符合题目要求,该考生在剩下的三个选项中,随机选了一个;还有两个题,每个题给出的四个选项,可判断有两个选项不符合题目要求,对于这两个题,该考生都是在剩下的两个选项中,随机选了一个选项.请你根据上述信息,解决下列问题:
个题,有一个题,因全然不理解题意,该考生在给出的四个选项中,随机选了一个;有一个题给出的四个选项,可判断有一个选项不符合题目要求,该考生在剩下的三个选项中,随机选了一个;还有两个题,每个题给出的四个选项,可判断有两个选项不符合题目要求,对于这两个题,该考生都是在剩下的两个选项中,随机选了一个选项.请你根据上述信息,解决下列问题:
(Ⅰ)在这次考试中,求该考生选择题部分得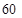 分的概率;
分的概率;
(Ⅱ)在这次考试中,设该考生选择题部分的得分为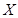 ,求
,求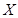 的数学期望.
的数学期望.
已知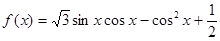 .
.
(Ⅰ)写出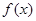 的最小正周期
的最小正周期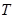 ;
;
(Ⅱ)求由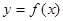
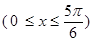 ,
,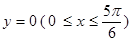 ,
,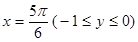 ,以及
,以及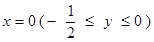 围成的平面图形的面积.
围成的平面图形的面积.
已知椭圆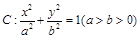 ,
,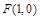 为其右焦点,离心率为
为其右焦点,离心率为 .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若点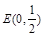 ,问是否存在直线
,问是否存在直线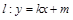 ,使
,使 与椭圆
与椭圆 交于
交于 两点,且
两点,且 .若存在,求出
.若存在,求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
已知等差数列 和公比为
和公比为
 的等比数列
的等比数列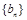 满足:
满足: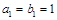 ,
,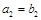 ,
, .
.
(Ⅰ)求数列 ,
,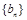 的通项公式;
的通项公式;
(Ⅱ)若数列 的前
的前 项和为
项和为 ,且对任意
,且对任意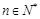 均有
均有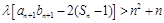 成立,试求实数
成立,试求实数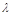 的取值范围.
的取值范围.
如图,已知四边形 为梯形,
为梯形, ,
, ,四边形
,四边形 为矩形,且平面
为矩形,且平面 平面
平面 ,
, ,点
,点 为
为 的中点.
的中点.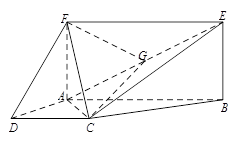
(Ⅰ)求证: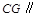 平面
平面 ;
;
(Ⅱ)求证:平面 平面
平面 ;
;
(Ⅲ)求三棱锥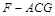 的体积.
的体积.