(本小题满分13分) 从4名文科教师和3名理科教师中任选3人担任班主任.(写出过程,最后结果用分数表示)
(1)求所选3人都是理科教师的概率;
(2)求所选3人中恰有1名理科教师的概率;
(3)求所选3人中至少有1名理科教师的概率.
已知函数f(x)=4cos ωx· (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π.
(1)求ω的值;
(2)讨论f(x)在区间 上的单调性.
上的单调性.
设全集 .
.
(1)解关于x的不等式 ;
;
(2)记A为(1)中不等式的解集,集合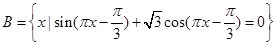 ,若
,若 恰有3个元素,求
恰有3个元素,求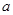 的取值范围.
的取值范围.
已知曲线C的极坐标方程是 ,以极点为平面直角坐标系的原点,极轴为轴的正半轴建立平面直角坐标系,直线L的参数方程是
,以极点为平面直角坐标系的原点,极轴为轴的正半轴建立平面直角坐标系,直线L的参数方程是 (t是参数)
(t是参数)
(1)将曲线C的极坐标方程和直线L参数方程转化为普通方程;
(2)若直线L与曲线C相交于M、N两点,且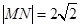 ,求实数m的值.
,求实数m的值.
如图⊙O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交⊙O于点N,过点N的切线交CA的延长线于P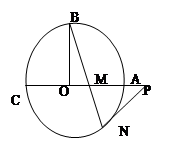
(1)求证:
(2)若⊙O的半径为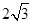 ,OA=
,OA= OM,求MN的长
OM,求MN的长
已知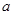 是实数,函数
是实数,函数 .
.
(1)若 ,求
,求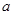 的值及曲线
的值及曲线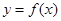 在点
在点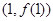 处的切线方程.
处的切线方程.
(2)求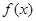 在
在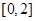 上的最大值.
上的最大值.