(本小题满分12分)
如图,在三棱锥P—ABC中,AB⊥ BC,AB =" BC" = kPA,点E、D分别是AC、PC的中点,EP⊥底面ABC.
BC,AB =" BC" = kPA,点E、D分别是AC、PC的中点,EP⊥底面ABC.
(1) 求证:ED∥平面PAB;
(2) 求 直线AB与平面PAC所成的角;
直线AB与平面PAC所成的角;
(3) 当k取何值时,E在平面PBC内的射影恰好为△PBC的重心?
已知命题 :方程
:方程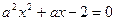 在[-1,1]上有解;命题
在[-1,1]上有解;命题 :只有一个实数
:只有一个实数 满足不等式
满足不等式 ,若命题“p或q”是假命题,求实数a的取值范围.
,若命题“p或q”是假命题,求实数a的取值范围.
(12分)如图,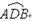 为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.
为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.
(1)建立适当的平面直角坐标系,求曲线C的方程;
(2)过D点的直线 l与曲线C相交于不同的两点M、N,且M在D、N之间,设
l与曲线C相交于不同的两点M、N,且M在D、N之间,设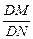 =λ,求λ的取值范围.
=λ,求λ的取值范围.
双曲线 (a>1,b>0)的焦距为2c,直线
(a>1,b>0)的焦距为2c,直线 过点(a,0)和(0,b),且点(1,0)到直线
过点(a,0)和(0,b),且点(1,0)到直线 的距离与点(-1,0)到直线
的距离与点(-1,0)到直线 的距离之和s≥
的距离之和s≥ c.求双曲线的离心率e的取值范围.
c.求双曲线的离心率e的取值范围.
假设关于某市房屋面积 (平方米)与购房费用
(平方米)与购房费用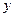 (万元),有如下的统计数据:
(万元),有如下的统计数据:
| x(平方米) |
80 |
90 |
100 |
110 |
| y(万元) |
42 |
46 |
53 |
59 |
由资料表明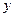 对
对 呈线性相关。
呈线性相关。
(1)求回归直线方程;
(2)若在该市购买120平方米的房屋,估计购房费用是多少?
公式:
某校从参加高一年级期末考试的学生中抽出60名学生,将其物理成绩(均为整数)分成六段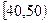 ,
, …
… 后画出如下频率分布直方图.观察图形的信息,回答下列问题:
后画出如下频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)估计这次考试的众数m与中位数n(结果保留一位小数);
(Ⅱ)估计这次考试的及格率(60分及以上为及格)和平均分.