已知椭圆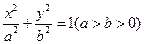 的两焦点
的两焦点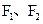 和短轴的两端点
和短轴的两端点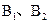 正好是一正方形的四个顶点,且焦点到椭圆上一点的最近距离为
正好是一正方形的四个顶点,且焦点到椭圆上一点的最近距离为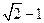 .
.
(1)求椭圆的标准方程;
(2)设P是椭圆上任一点,MN 是圆C: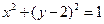 的任一条直径,求
的任一条直径,求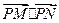 的最大值.
的最大值.
(本小题满分12分) 如图,四棱锥
如图,四棱锥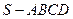 的底面是矩形,
的底面是矩形,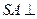 底面
底面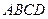 ,P为BC边的中点,SB与
,P为BC边的中点,SB与
平面ABCD所成的角为45°,且AD=2,SA=1.
(1)求证: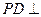 平面SAP;
平面SAP;
(2)求二面角A-SD-P的大小.
定义数列如下: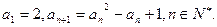
证明:(1)当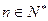 时,恒有
时,恒有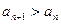 成立;
成立;
(2)当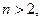 且
且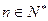 时,有
时,有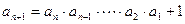 成立;
成立;
(3)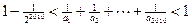 .
.
设直线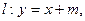 双曲线
双曲线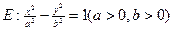 ,双曲线的离心率为
,双曲线的离心率为 ,
,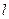 与
与 交于
交于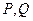 两点,直线
两点,直线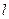 与
与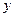 轴交于点
轴交于点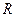 ,且
,且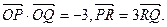
(1)证明: ;(2)求双曲线
;(2)求双曲线 的方程;(3)若点
的方程;(3)若点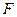 是双曲线
是双曲线 的右焦点,
的右焦点,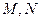 是双曲线上两点,且
是双曲线上两点,且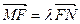 ,求实数
,求实数 的取值范围.
的取值范围.
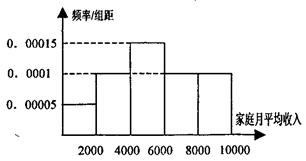
某校调查了高三年级1000位同学的家庭月平均收入情况,得到家庭月平均收入频率分布直方图如图,
(1)某企业准备给该校高三同学发放助学金,发放规定如下:家庭收入在4000元以下的每位同学得助学金2000元,家庭收入在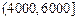 (元)间的每位同学得助学金1500元,家庭收入在
(元)间的每位同学得助学金1500元,家庭收入在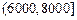 (元)间的每位同学得助学金1000元,家庭收入在
(元)间的每位同学得助学金1000元,家庭收入在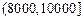 (元),间的同学不发助学金,记该年级某位同学所得助学金为
(元),间的同学不发助学金,记该年级某位同学所得助学金为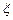 元,写出
元,写出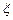 的分布列,并计算该企业发放这个年级的助学金约需要的资金;
的分布列,并计算该企业发放这个年级的助学金约需要的资金;
(2)记该年级某班同桌两位同学所得助学金之差的绝对值为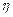 元,求
元,求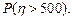
设函数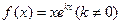 (Ⅰ)求曲线
(Ⅰ)求曲线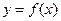 在点
在点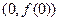 处的切线方程;(Ⅱ)求函数
处的切线方程;(Ⅱ)求函数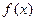 的单调区间;(Ⅲ)若函数
的单调区间;(Ⅲ)若函数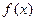 在区间
在区间 内单调递增,求
内单调递增,求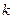 的取值范围.
的取值范围.