(本小题满分12分)
椭圆 与直线
与直线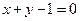 相交于
相交于 、
、 两点,且
两点,且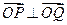 (
(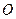 为坐标原点).
为坐标原点).
(Ⅰ)求证: 等于定值;
等于定值;
(Ⅱ)当椭圆的离心率 时,求椭圆长轴长的取值范围.
时,求椭圆长轴长的取值范围.
已知函数
(1)若 求
求 的单调区间及
的单调区间及 的最小值;
的最小值;
(2)若 ,求
,求 的单调区间;
的单调区间;
(3)试比较) 的大小,
的大小, ,并证明你的结论。
,并证明你的结论。
定长为3的线段AB两端点A、B分别在 轴,
轴, 轴上滑动,M在线段AB上,且
轴上滑动,M在线段AB上,且
(1)求点M的轨迹C的方程;
(2)设过 且不垂直于坐标轴的动直线
且不垂直于坐标轴的动直线 交轨迹C于A、B两点,问:线段
交轨迹C于A、B两点,问:线段 上是否存在一点D,使得以DA,DB为邻边的平行四边形为菱形?作出判断并证明。
上是否存在一点D,使得以DA,DB为邻边的平行四边形为菱形?作出判断并证明。
某商店投入38万元经销某种纪念品,经销时间共60天,为了获得更多的利润,商店将每天获得的利润投入到次日的经营中,市场调研表明,该商店在经销这一产品期间第 天的利润
天的利润 (单位:万元,
(单位:万元, ),记第
),记第 天的利润率
天的利润率 ,例如
,例如
求
 的值;
的值;求第
 天的利润率
天的利润率 ;
;该商店在经销此纪品期间,哪一天的利润率最大?并求该天的利润率。
如图,在直角梯形ABCD中,AD//BC, ,当E、F分别在线段AD、BC上,且
,当E、F分别在线段AD、BC上,且 ,AD=4,CB=6,AE=2,现将梯形ABCD沿EF折叠,使平面ABFE与平面EFCD垂直。
,AD=4,CB=6,AE=2,现将梯形ABCD沿EF折叠,使平面ABFE与平面EFCD垂直。判断直线AD与BC是否共面,并证明你的结论;
当直线AC与平面EFCD所成角为多少时,二面角A—DC—E的大小是60°。

2010年5月1日,上海世博会将举行,在安全保障方面,警方从武警训练基地挑选防爆警察,从体能、射击、反应三项指标进行检测,如果这三项中至少有两项通过即可入选。假定某基地有4名武警战士(分别记为A、B、C、D)拟参加挑选,且每人能通过体能、射击、反应的概率分别为 。这三项测试能否通过相互之间没有影响。
。这三项测试能否通过相互之间没有影响。求A能够入选的概率;
规定:按人选人数得训练经费(每人选1人,则相应的训练基地得到3000元的训练经费),求该基地得到训练经费的分布列与数学期望。