(本小题满分16分)设数列 的通项公式为
的通项公式为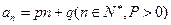 . 数列
. 数列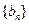 定义如下:对于正整数m,
定义如下:对于正整数m,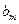 是使得不等式
是使得不等式 成立的所有n中的最小值.
成立的所有n中的最小值.
(Ⅰ)若 ,求
,求 ;(Ⅱ)若
;(Ⅱ)若 ,求数列
,求数列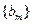 的前2m项和公式;
的前2m项和公式;
(Ⅲ)是否存在p和q,使得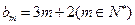 ?如果存在,求p和q的取值范围;如果不存在,请说明理由.
?如果存在,求p和q的取值范围;如果不存在,请说明理由.
(本小题满分14分)设 为奇函数,
为奇函数, 为常数.
为常数.
(1)求 的值;
的值;
(2)求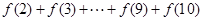 的值;
的值;
(3)若对于区间[3,4]上的每一个 的值,不等式
的值,不等式 >
> 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分12分)已知函数 ,
, ,
,
(1)判断函数 的奇偶性,并证明;
的奇偶性,并证明;
(2)判断 的单调性,并说明理由。(不需要严格的定义证明,只要说出理由即可)
的单调性,并说明理由。(不需要严格的定义证明,只要说出理由即可)
(3)若 ,方程
,方程 是否有根?如果有根
是否有根?如果有根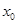 ,请求出一个长度为1的区间
,请求出一个长度为1的区间 ,使
,使 ;如果没有,请说明理由。(注:区间
;如果没有,请说明理由。(注:区间 的长度=
的长度= )
)
(本小题满分12分)已知
(1)求 的最小值;
的最小值;
(2)求 的值域。
的值域。
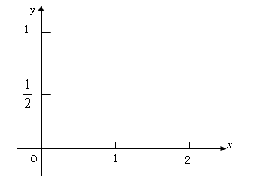
(本小题满分12分)如下左图,已知底角为450的等腰三角形ABC,底边AB的长为2,当一条垂直于AB的直线L从左至右移动时,直线L把三角形ABC分成两部分,令AD=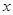 ,
,
(1) 试写出左边部分的面积 与x的函数解析式;
与x的函数解析式;
(2) 在给出的坐标系中画出函数的大致图象。 
(本小题满分12分)设全集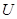 =
=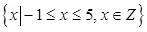 ,
,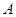 =
=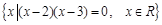 ,
, 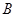 =
=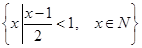 ,分别求
,分别求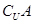 、
、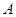
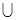
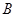 、
、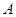
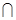
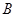 .
.