(本小题满分12分)设全集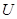 =
=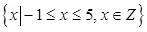 ,
,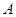 =
=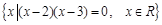 ,
, 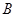 =
=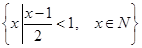 ,分别求
,分别求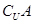 、
、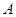
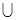
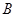 、
、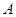
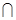
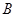 .
.
(本小题满分12分)
如图,在四棱锥 中,
中, ,
,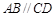 ,
, ,平面
,平面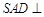 平面
平面 ,
, 是线段
是线段 上一点,
上一点,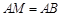 ,
,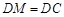 ,
,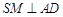 .
.
(Ⅰ)证明: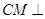
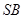 ;
;
(Ⅱ)设三棱锥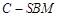 与四棱锥
与四棱锥 的体积分别为
的体积分别为 与
与 ,求
,求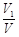 的值.
的值.
(本小题满分12分)下图为某地区2013年1月到2014年1月鲜蔬价格指数的变化情况:
记 本月价格指数
本月价格指数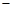 上月价格指数. 规定:当
上月价格指数. 规定:当 时,称本月价格指数环比增长;
时,称本月价格指数环比增长;
当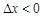 时,称本月价格指数环比下降;当
时,称本月价格指数环比下降;当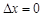 时,称本月价格指数环比持平.
时,称本月价格指数环比持平.
(Ⅰ) 比较2013年上半年与下半年鲜蔬价格指数月平均值的大小(不要求计算过程);
(Ⅱ) 直接写出从2013年2月到2014年1月的12个月中价格指数环比下降的月份. 若从这12个月中随机选择连续的两个月进行观察,求所选两个月的价格指数都环比下降的概率;
(Ⅲ) 由图判断从哪个月开始连续三个月的价格指数方差最大. (结论不要求证明)
(本小题满分12分)
已知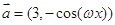 ,
,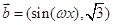 ,其中
,其中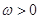 ,函数
,函数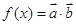 的最小正周期为
的最小正周期为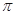 .
.
(Ⅰ)求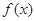 的单调递增区间;
的单调递增区间;
(Ⅱ)在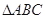 中,角
中,角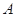 ,
,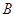 ,
,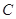 的对边分别为
的对边分别为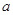 ,
,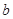 ,
,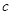 .且
.且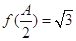 ,
,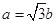 ,求角
,求角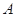 、
、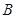 、
、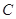 的大小.
的大小.
已知在直角坐标系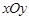 中,曲线
中,曲线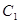 的参数方程为
的参数方程为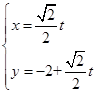
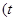 为参数).在极坐标系(与直角坐标取相同的长度单位,且以原点
为参数).在极坐标系(与直角坐标取相同的长度单位,且以原点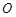 为极点,
为极点,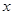 轴的非负半轴为极轴)中,曲线
轴的非负半轴为极轴)中,曲线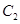 的方程为
的方程为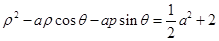 ,
,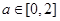 .
.
(Ⅰ)求曲线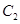 直角坐标方程,并说明方程表示的曲线类型;
直角坐标方程,并说明方程表示的曲线类型;
(Ⅱ)若曲线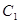 、
、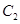 交于A、B两点,定点
交于A、B两点,定点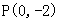 ,求
,求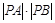 的最大值.
的最大值.
如图,圆O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交圆O于N,点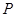 是线段
是线段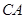 延长线上一点,连接PN,且满足
延长线上一点,连接PN,且满足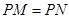
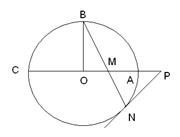
(Ⅰ)求证: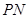 是圆O的切线;
是圆O的切线;
(Ⅱ)若圆O的半径为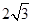 ,OA=
,OA=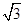 OM,求MN的长.
OM,求MN的长.