2015年春节期间，高速公路车辆较多．某调查公司在一服务区从七座以下小型汽车中，按进服务区的先后每间隔
辆就抽取一辆的抽样方法，抽取了
名驾驶员进行调查，将他们在某段高速公路上的车速（km/t）分成6段：
，
，
，
，
，
后得到如图４的频率分布直方图．问：
（1）该公司在调查取样中，用到的是什么抽样方法？
（2）求这40辆小型汽车车速的众数和中位数的估计值；
（3）若从车速在
中的车辆中任取2辆，求抽出的这两辆车中速度在中的车辆数
的分布列及其数学期望．
已知函数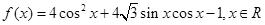
.
（1）求函数的最小正周期、最大值及取最大值时自变量的取值集合；
（2）在△ABC中，角A，B，C的对边分别是a，b，c；若a，b，c成等比数列，且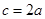
，求
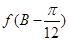的值.
设函数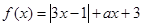
.
（1）若
时，解不等式
；
（2）若函数
有最小值，求a的取值范围.
在直角坐标系中，以原点为极点，x轴的正半轴为极轴建立极坐标系，已知曲线C：
，过点P（-2，-4）的直线
的参数方程为
（t为参数）与C分别交于M，N.
（1）写出C的平面直角坐标系方程和的普通方程；
（2）若
，
，
成等比数列，求a 的值.
已知PQ与圆O相切于点A，直线PBC交圆于B、C两点，D是圆上一点，且AB∥CD，DC的延长线交PQ于点Q.
（1）求证：
（2）若AQ=2AP，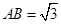
,BP=2，求QD.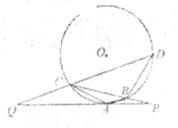
已知函数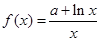
在点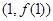
处的切线与x轴平行.
（1）求实数a的值及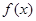
的极值；
（2）是否存在区间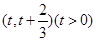
，使函数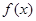在此区间上存在极值和零点？若存在，求实数t的取值范围，若不存在，请说明理由；
（3）如果对任意的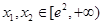
，有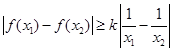
，求实数k的取值范围.